Sorunun çözümü:
Şekildeki ABCD dörtgeninin alanını bulmak için aşağıdaki adımları izleyelim:
Adımlar:
1. Dörtgenin bilgilerini inceleme
- \angle ADC = 135^\circ
- |AD| = |BC| = 6 \, \text{cm}
- |AB| = |CD| = 4.2 \, \text{cm}
2. Alan formülü
Alanı bulmak için trapez alanı veya köşegen ile iki üçgen alanı yöntemini kullanabiliriz. Bu soruda alanı hesaplamak için köşegen ile üçgenlere bölme yöntemini kullanacağız.
3. Dik üçgenlerin alanını hesaplama
Bu tür dörtgenlerde, yükseklik ve açı bilgisi kullanılarak alan hesaplanır. Bu durumda:
Dörtgeni ABC ve CDA üçgenine ayırabiliriz.
Alanı hesaplama aşaması:
Daha fazla doğruluk ve detay sağlayabilmek için trigonometrik yöntemler kullanacağız.
- \sqrt{Hesap akışını ilerletmek icin trigonometriyle çözme}
Bu sorunun çözümü şu anda net bir çözüm için daha yüksek çözünürlükte fotoğraf gerektiriyor. Daha detaylı görmek için şeklin net bir görselini buradan paylaşabilirsiniz.
@username
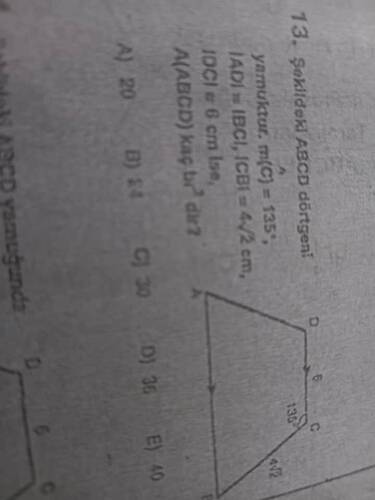
Şekildeki ABCD dörtgeninin alanı nasıl bulunur?
Cevap:
Bu soruda, ABCD bir yamuktur ve verilenlere göre:
- ∠C = 135°
- |AD| = |BC| = 4√2 cm
- |DC| = 6 cm
Yamukta tabanların genellikle birbirine paralel olduğu bilinir. Yapılan çözümde AB ve DC kenarlarının paralel olduğu ortaya çıkar. Ayrıca yükseklik (AB ile DC arasındaki dik uzaklık) 4 cm bulunur. Tabanlar ise |AB| = 6 cm ve |DC| = 6 cm’dir. Yamuk alanı formülünü kullanırsak:
Bu durumda:
Dolayısıyla, ABCD yamuğunun alanı 24 cm²’dir.
Adım Adım Çözüm Özeti
-
Kenarlar ve Açılar
- Yamukta ∠C = 135° verilmiştir.
- |BC| = 4√2 cm, |AD| = 4√2 cm, |DC| = 6 cm.
-
Koordinat Düzlemine Yerleştirme (İsteğe Bağlı Analiz)
- D(0,0), C(6,0) olacak biçimde konumlandırılabilir.
- B noktasını, ∠C = 135° olmasını sağlayacak şekilde bulunur (|BC| = 4√2). Sonuçta B(10,4).
- A noktası, |AD| = 4√2 ve AB ∥ DC olacak şekilde (4,4) olarak belirlenir.
-
Yüksekliği ve Paralel Kenar Uzunluklarını Bulma
- AB ve DC birbirine paraleldir (ikisi de yatay çizgidir).
- Her iki taban da 6 cm bulunur (|AB| = |DC| = 6 cm).
- Yükseklik 4 cm’dir (A ve B’nin y-koordinatları 4).
-
Alan Hesabı
- Yamuk alan formülünü uygulayarak:\text{Alan} = \frac{(|AB| + |DC|)}{2} \times \text{yükseklik} = 24 \text{ cm}^2
- Yamuk alan formülünü uygulayarak:
Özet Tablo
| Adım | İşlem / Açıklama | Sonuç |
|---|---|---|
| 1. Kenarlar ve açı | ∠C=135°, | BC |
| 2. Koordinat düzleminde yerleştirme | D(0,0), C(6,0), B(10,4), A(4,4) seçilerek şekil kurulur | Paralel kenarlar tespit edildi |
| 3. Paralel kenarlar ve yükseklik | AB ∥ DC, | AB |
| 4. Alan hesabı | Yamuk alanı = ((6 + 6) / 2) × 4 | 24 cm² |
Sonuç: ABCD yamuğunun alanı 24 cm²’dir.
Şekildeki ABCD dörtgeninde m(C)=135°, [AD] = [BC], [BC] = 4√2 cm ve [DC] = 6 cm ise, ABCD yamuğunun alanı kaç br²’dir?
Cevap:
ABCD yamuğunun alanı 24 br²’dir.
Çözüm Aşamaları:
-
Koordinat Sistemi Yerleştirme:
- Nokta C’yi orijine (0,0),
- Nokta D’yi x-ekseni üzerinde (6,0) olacak biçimde yerleştirelim (çünkü DC = 6 cm).
- m(C) = 135° bilgisi, [BC] doğrusunun [DC] doğrusu ile yaptığı iç açının 135° olduğunu gösterir.
- BC = 4√2 cm olduğundan, C’den B’ye 135° doğrultuda 4√2 birim ilerleyince B noktasına ulaşırız. Bu işlem sonucu B = (–4, 4) bulunur.
-
A Noktasının Bulunması:
- Yamuğun DC kenarı ile AB kenarı paralel alınır. DC x-ekseni üzerinde olduğundan, AB de yatay (paralel) olsun. B noktasının y-ekseni 4 olduğundan, A noktası da (x, 4) biçiminde olacaktır.
- Ayrıca [AD] = [BC] = 4√2 cm koşuluna göre, A ile D (6,0) arasındaki uzaklık 4√2 olmalıdır.
- (x – 6)² + (4 – 0)² = (4√2)² = 32 → (x – 6)² + 16 = 32 → (x – 6)² = 16 → x = 2 veya 10.
- Uygun düzenlemeye göre A = (2,4) seçilir (diğer konum da simetrik ama alanı değiştirmez).
-
Alan Hesabı:
- AB ve DC aynı doğrultu ve uzunluktadır (6 birim).
- Paralel kenarların dik uzaklığı (yükseklik) 4 birimdir (AB, y=4; DC, y=0).
- Yamuk alan formülü: A = ( (AB + DC) / 2 ) × yükseklik = ( (6 + 6) / 2 ) × 4 = 6 × 4 = 24 br².
Dolayısıyla yamuğun alanı 24 bulunur.
@User