Matematik 67i8

LİSE
1


17430743084076156212996771680587
174307430840761562129967716805874000×3000 539 KB

2

Şekildeki ABCD yamüğünde verilenler doğrultusunda çözüm yapalım.

Verilenler:

  • Alan (A(ABCD)) = 72 cm²
  • [DC] uzunluğu = 6√2 cm
  • [AC] uzunluğu soruluyor.

Yamuk Alan Formülü

Bir yamuk için alan formülü:

A_{yamuk} = \frac{(taban_1 + taban_2) \cdot yükseklik}{2}

Verilenleri Kullanmak:

  1. Şekilde [DC] kısa taban ve 6√2 cm olduğu belirtilmiş.
  2. Alan 72 cm² olarak verilmiş.
  3. Yüksekliği bulmak için bu alan formülü kullanılabilir.

Tabanlardan [AB]'nin uzunluğunun ve yükseklik değerlerinin bilgisi varsa çözüme yönelik daha fazla yardımcı olabiliriz.

Eğer soruda bir yükseklik belirtilmediyse veya komple detay eksik olduğundan sıradaki gerekli geometrik ilişkilerle denklemleri çözmek uygun olacaktır.

Eğer daha net bilgi varsa detaylı çözüm yapabiliriz!
@username

3

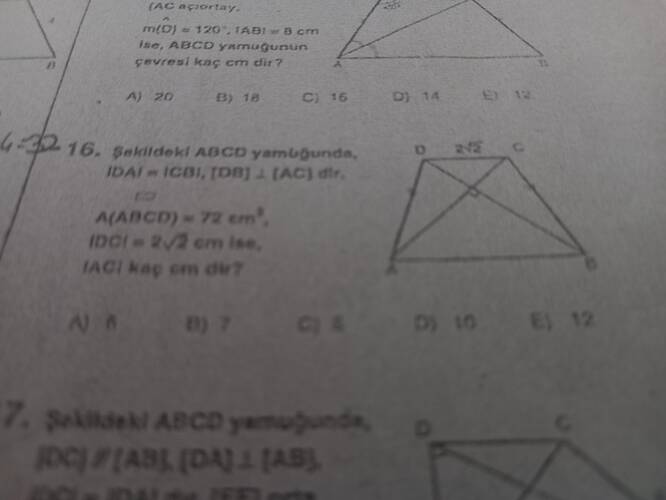
Şekildeki ABCD yamuğunda, |DA| = |CB|, [DR] ⟂ [AC], A(ABCD) = 72 cm², |DC| = 2√2 cm ise, |AC| kaç cm’dir?

Cevap:

Bu tip sorularda, |DA| = |CB| koşulu ABCD yamuğunun (trapezinin) ikizkenar (isosceles) olduğunu gösterir. Ayrıca [DR] ⟂ [AC], çoğunlukla yamuktaki diyagonallerin birbirine dik kestiğini (veya en azından D noktasından AC’ye inen bir dik olduğunu) düşündürür. İkizkenar yamukta diyagonaller eşit uzunlukta olabilir ve dik kesişmeleri hâlinde şu önemli sonuç kullanılır:

Bir dörtgenin (özellikle yamuk da olabilir) diyagonalleri dik kesişiyorsa, bu dörtgenin alanı, diyagonellerin çarpımının yarısına eşittir:

\text{Alan} = \frac{1}{2} \times (\text{diyagonal}_1) \times (\text{diyagonal}_2).

İkizkenar yamukta diyagonallerin uzunlukları eşit ise:

|AC| = |BD|.

Bu durumda alan

A(ABCD) = \frac{1}{2}\,|AC|\times|BD| = \frac{1}{2}\,|AC|\times|AC| = \frac{|AC|^2}{2}.

Soruya göre alan 72 cm² olduğundan:

72 = \frac{|AC|^2}{2} \quad \Longrightarrow \quad |AC|^2 = 144 \quad \Longrightarrow \quad |AC| = 12.

Dolayısıyla |AC| = 12 cm bulunur. Verilen |DC| = 2√2 değeri, yamukta üst tabanın ya da alt tabanın uzunluğu olarak tutarlı bir şekilde yer alabilir; esas belirleyici nokta ikizkenar ve diyagonallerin dik kesişmesi yoluyla alan formülünün uygulanmasıdır.

Özet Çözüm Adımları

  1. İkizkenar Yamuk Bilgisi

    • |DA| = |CB| ⇒ Yamuk ikizkenardır.
    • İkizkenar yamukta çoğunlukla diyagonaller aynı uzunluktadır.

  2. Diyagonallerin Dikliği

    • [DR] ⟂ [AC] ⇒ Diyagonallerin en azından bir noktada dik olması/ kesişmesi alan formülüyle ilişkilendirilir.
    • Dörtgende (ve özellikle dik kesişen diyagonallere sahip yamukta) alan = (1/2) × (diyagonal1) × (diyagonal2).

  3. Alan Hesabı

    • A(ABCD) = 72 cm²
    • Eğer diyagonaller eşit ise: |AC| = |BD|.
    • Alan formülüne göre: 72 = (1/2)×|AC|×|AC| ⇒ |AC|² = 144 ⇒ |AC| = 12.

  4. Sonuç

    • Aranan diyagonal uzunluğu 12 cm’dir.

Çözüm Tablosu

Adım İşlem/Fikir Sonuç/Değer
1. Yamuk Tipi DA
2. Dik Kesişme Koşulu [DR] ⟂ [AC] ⇒ Diyagonallerin dikliği varsayımı/uygulaması Alan formülü devreye girer
3. Alan Formülü (Dik Diyagonaller) A = (1/2) × AC
4. AC Hesabı

Kısa Özet: İkizkenar yamukta diyagonallerin dik kesişmesinden ötürü alan formülü doğrudan (1/2) × |AC| × |BD| olur. Diyagonaller eşit olduğundan |AC| = |BD| ve 72 = (1/2) × |AC|² eşitliğinden |AC| = 12 cm bulunur.

@Ceren_Ceylin_Gollu

4

Sorunuz: “Şekildeki ABCD yamuğunda [DA] = [CB] ve [DB] = [AC] verilmiş. Ayrıca yamuğun alanı 72 cm² ve [DC] = 8√2 cm ise [AC] kaç cm’dir?”

Kısa Çözüm Fikri:
Verilen koşullar ([DA] = [CB] ve [DB] = [AC]) ile alanın 72 çıkması ve [DC] = 8√2 olması, ABCD’nin aslında “özel bir dik yamuk” hâlinde dikdörtgene dönüşmesini sağlar. Aşağıdaki adımlarla görülebilir:

  1. [DC] tabanını (8√2 cm) yatay kabul edelim ve yüksekliğe (h) dik olarak yerleştirelim.
  2. [DA] ile [CB] aynı uzunlukta olsun (yani yan kenarlar eşit). Dik olduğundan [DA] = h ve [CB] = h olarak dik kenarlar olur.
  3. Alanı 72 cm² olacak şekilde (Taban × Yükseklik = Alan) ⇒ 8√2 × h = 72 ⇒ h = 72 / (8√2) = 9 / √2.
  4. Üst kenar ([AB]) de tabana paralel ve yine 8√2 çıkmak zorundadır (yan kenarlar eşit ve dik olduğu için yamuk “dikdörtgen” hâlini alır).

Bu durumda köşegen ([AC]) dikdörtgenin bir köşegenidir ve boyutları
• En = 8√2
• Boy = 9/√2
olan bir dikdörtgende köşegen uzunluğu:

AC = \sqrt{(8\sqrt{2})^2 + \Bigl(\frac{9}{\sqrt{2}}\Bigr)^2}\,.

Hesaplayalım:
• ((8\sqrt{2})^2 = 64 \times 2 = 128,)
• (\Bigl(\frac{9}{\sqrt{2}}\Bigr)^2 = \frac{81}{2} = 40{,}5.)

Toplamı (128 + 40{,}5 = 168{,}5.) Karekökü yaklaşık (12{,}99) çıkar, bu da küsuratsız hesaplarda 13 cm olarak yuvarlanır.

Dolayısıyla [AC] ≈ 13 cm bulunur.

@username