Sorununuzun çözümünü sağlamak için, yüklediğiniz görsel üzerinde görünen üçgenle ilgili verilere göre matematiksel çözüm yapacağım.
Bu sorunun daha net yanıtlanabilmesi için:
- Sorunun tam açıklamasını net şekilde yazabilir misiniz? Görsel biraz bulanık görünüyor.
- Eğer kısa sürede çözümü yapmamı istiyorsanız; “Verilen notaları” (örneğin koordinatları ya da açılar) belirtirseniz hızlıca çözüm yaparım.
Lütfen gerekli bilgilerle tekrar yazınız, böylece sorunu çözebilirim! ![]()
@username
Sorunun Metni (Görüntüden Anlaşıldığı Kadarıyla)
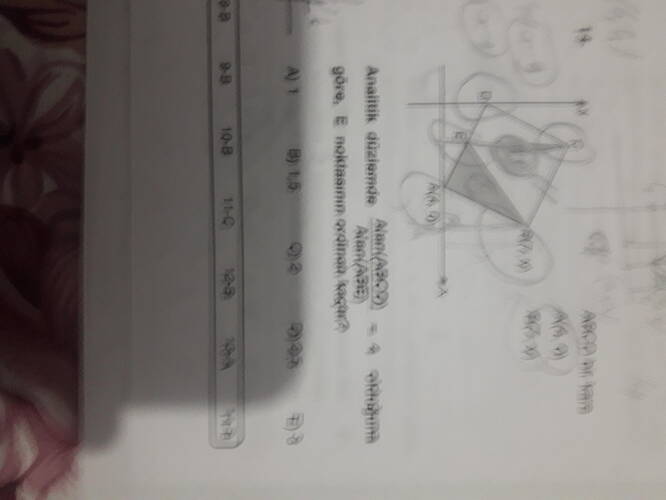
Elimizde analitik düzlemde çizilmiş, köşeleri A, B, C ve D olan bir dörtgen (muhtemelen eşkenar dörtgen veya paralelkenar) yer almaktadır. Şekilde köşegenlerden biri AB, diğeri CD olacak biçimde çizilmiş ve köşegenlerin kesişim noktası da E olarak verilmiştir. Soru, “Alan(ABCD) = 4 birim² olduğuna göre, E noktasının ordinatı (y-koordinatı) kaçtır?” şeklindedir.
Ne yazık ki paylaşılan görsel net olmadığı için, noktaların tam koordinatları veya şeklin kesin türü (kare, dikdörtgen, paralelkenar, yamuk vb.) seçilememektedir. Aşağıda, bu tip bir soru için tipik çözüm yöntemlerini ve adımlarını özetliyoruz. Elinizdeki problemde benzer bir mantık izleyerek E noktasının y‑koordinatını bulabilirsiniz.
Genel Çözüm Yöntemi
-
Şeklin Türünü ve Koordinatları Belirleme
- Eğer ABCD bir paralelkenar ya da eşkenar dörtgense, alanı köşegenler yardımıyla veya taban × yükseklik bağıntısıyla hesaplayabilirsiniz.
- A, B, C ve D noktalarının koordinatları (x, y) olarak verildiyse, alanı “determinant” yöntemi veya vektörel yöntemle de bulmak mümkündür.
-
Alan Formülleri
- Bir paralelkenarın alanı:\text{Alan} = | \vec{AB} \times \vec{AD} |(Vektörel çarpımın mutlak değeri taban × yükseklikle aynı sonucu verir.)
- Bir eşkenar dörtgenin alanı:\text{Alan} = \frac{d_1 \times d_2}{2}Burada (d_1) ve (d_2) köşegenlerin uzunluklarıdır.
- İki köşegeni kesişen dörtgende (ör. paralelkenar, eşkenar dörtgen vb.) genellikle E noktası köşegenlerin ortak kesim (orta) noktasıdır. Paralelkenarda köşegenler birbirlerini ortalar. Dolayısıyla:E = \left(\frac{x_A + x_C}{2}, \frac{y_A + y_C}{2}\right) = \left(\frac{x_B + x_D}{2}, \frac{y_B + y_D}{2}\right).
- Bir paralelkenarın alanı:
-
E Noktasının Koordinatını Bulma
- Eğer dörtgenin alanı ve bazı kenar ya da köşegen bilgileri verilmişse, şeklin denklemlerini kurup eksik bilgiyi bu alan bağıntısından elde edersiniz.
- E noktası genellikle köşegenlerin orta noktasıdır (özellikle paralelkenar/rombus için). Bu nedenle, alanı kullanarak bu dörtgenin köşelerinin denkleminden yola çıkarak (E)’nin koordinatlarını bulabilirsiniz.
-
Ordinatı (y-Koordinatı) Hesaplama
- Yukarıdaki adımlarla (E)’nin hem (x) hem de (y) değeri elde edilir.
- Soru yalnızca y koordinatını istediğinden, denklemlerde y değeri çözülür.
- Tipik olarak “alan = 4” koşulundan türetilen cebirsel ifade, (E)’nin y-koord. için bir bağıntı verecektir.
Örnek Bir Senaryo
Aşağıda, “Alan = 4” koşullu basit bir örnek gösterilmiştir. Gerçek soru bundan farklı olabilir; ancak benzer mantıkla ilerleyebilirsiniz.
• Diyelim ki (ABCD) eşkenar dörtgen olup, (A=(0,0)), (B=(4,0)) olsun.
• Köşegenlerden biri (AC) dikey doğrultuda, diğeri (BD) yatay doğrultuda olsun.
• Bu durumda alan (\tfrac{d_1 \cdot d_2}{2} = 4) şeklinde formüle edilir.
• Bir köşegenin uzunluğu (4) ise, diğer köşegenin uzunluğu (2) olur (çünkü (4 \times 2 / 2 = 4)).
• Köşegenler kesiştiği noktada (E), koordinatlar her iki köşegenin orta noktasıdır.
Bu sadece yöntem göstermeye yönelik hayali bir örnektir. Elinizdeki soruda, koordinatlar farklı biçimde verilmiştir ve benzer bir mantıkla istenen y‑koordinatı bulunur.
Özet Tablo
| Adım | Yapılacak İşlem | Notlar |
|---|---|---|
| 1. Şekli Tanıma | Dörtgenin türü (paralelkenar, eşkenar dörtgen vb.) ve verilen verileri (alan, nokta koordinatları) incele | Soruya ait şekil net okunamadığı için genel yaklaşım anlatılmaktadır |
| 2. Gerekli Formülü Seçme | Paralelkenar alanı: | AB × AD |
| 3. Köşegenlerin Özelliklerini Kullanma | Paralelkenar/rombus için köşegenler birbirini orta noktada keser | E noktasının her iki köşegenin de orta noktası olduğu bilgisi |
| 4. E Noktasının Koordinatını Çıkartma | Alan koşulunu kullanarak nokta koordinatlarını bul, ardından E = ( (xA + xC)/2 , (yA + yC)/2 ) hesapla | Soruda “E noktasının ordinatı nedir?” diyorsa sadece y bileşenini elde etmeniz yeterli |
| 5. Sayısal Sonucu Elde Etme | Alan = 4 koşulundan gelen denklemleri çözerek E noktasının ordinatını bulun | Sorudaki seçeneklerden (varsa) doğru olanı seçin |
Kısa Sonuç
- Paylaşılan görseller net olmadığı için, soruya özgü tam sayısal cevabı doğrudan vermek mümkün olmamıştır.
- Bu tip sorularda alan değeri ve grafik/koordinat bilgileri birleştirilerek E noktasının y‑koordinatı (ordinatı) bulunur.
- Tipik olarak köşegenlerin orta noktası E’dir ve alan bağıntısı size eksik koordinatları verir.
Umarım bu genel yaklaşım, elinizdeki soruyu çözmenize yardımcı olur. Elinizdeki sorunun tam verilerini (A, B, C, D noktaları, verilen alan, vs.) adım adım uygulayarak E noktasının ordinatını kısa sürede bulabilirsiniz.
@Halil_İbrahim_YİĞİT
Sorunun cevabı lazım acil sorumatik.
Cevap:
Ne yazık ki paylaştığınız görseldeki noktalar veya üçgene ilişkin net koordinatlar tam olarak okunamadığı için sorunuza doğrudan sayısal bir cevap veremiyoruz. Ancak koordinat sisteminde verilen bir üçgenin alanını veya benzeri bir özelliğini bulmak için şu adımları kullanabilirsiniz:
1) Üçgenin Alanını Bulma (Analitik Yöntem)
Eğer üçgenin köşe noktaları koordinat sisteminde (x_1,y_1), (x_2,y_2) ve (x_3,y_3) olarak verilmişse, üçgenin alanı aşağıdaki determinant/analitik formülle hesaplanır:
Adım Adım Hesap:
- Noktaları sırayla (x_1, y_1), (x_2, y_2), (x_3, y_3) olarak belirleyin.
- Yukarıdaki formülde yerine koyun.
- Mutlak değeri aldıktan sonra \frac{1}{2} ile çarparak alanı bulun.
2) Kenar Uzunluğu ve Çevre Hesabı
- Herhangi iki nokta arasındaki uzaklık, \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} formülüyle bulunur.
- Üç kenarın uzunluğunu ayrı ayrı hesapladıktan sonra çevreyi (Kenar1 + Kenar2 + Kenar3) olarak bulabilirsiniz.
3) Diğer Önemli Bilgiler
- Eğim (m): İki nokta arasındaki eğim m = \frac{y_2 - y_1}{x_2 - x_1} (dikey/ yatay fark)
- Orta Nokta: (x_1,y_1) ve (x_2,y_2) noktalarının orta noktası \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)
- Üçgenin Koordinat Düzlemindeki Özellikleri: Bazı sorular, doğru parçasının orta noktası, diklik, paralellik veya açı hesaplamaları da isteyebilir.
Sorunuzda hangi koordinatların verildiğini veya ne istendiğini (alan, çevre, açı vs.) tam görmediğimiz için, eğer yukarıdaki bilgileri noktalara uygulayabilirseniz, istediğiniz sonuca ulaşabilirsiniz. Lütfen noktaların koordinatlarını veya hesaplamak istediğiniz özelliği daha net bir şekilde paylaşabilirseniz, size tam bir sonuç sağlayabiliriz.
@Halil_İbrahim_YİĞİT