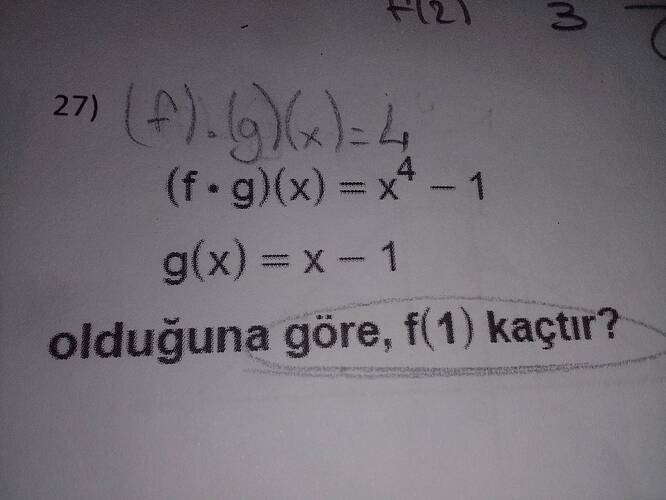Açıklamaya göre, (f \cdot g)(x) = f(x) \cdot g(x) şeklindedir. Soruda verilen bilgilere göre:
$$(f \cdot g)(x) = x^4 - 1 \quad \text{ve} \quad g(x) = x - 1$$
Şimdi f(x)'i bulalım.
$$f(x) \cdot g(x) = x^4 - 1$$
Bu durumda, g(x) = x - 1 olduğu için,
$$f(x) \cdot (x - 1) = x^4 - 1$$
Şimdi, f(x)'i bulmak için her iki tarafı x - 1'e bölelim:
f(x) = \frac{x^4 - 1}{x - 1}
x^4 - 1 ifadesi x^4 - 1 = (x^2 + 1)(x^2 - 1) ve ardından x^2 - 1 = (x - 1)(x + 1) şeklinde çarpanlarına ayrılır.
x^4 - 1 = (x^2 + 1)(x - 1)(x + 1)
Şimdi f(x)'i yerine koyalım:
f(x) = \frac{(x^2 + 1)(x - 1)(x + 1)}{x - 1}
x - 1'ler sadeleşir:
f(x) = (x^2 + 1)(x + 1)
Bu ifadede f(1)'i bulalım:
f(1) = (1^2 + 1)(1 + 1) = (1 + 1)(2) = 2 \times 2 = 4
Bu durumda f(1) değeri 4’tür.