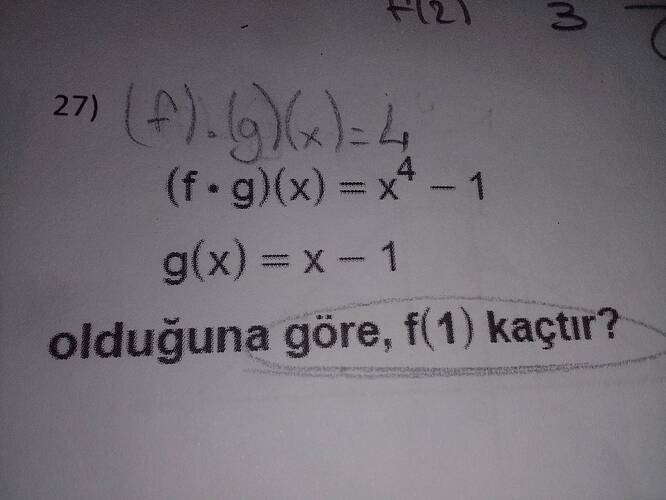F.g verilmiş f(1)=?

YKS TYT
1

IMG_20241204_180133
IMG_20241204_1801333264×2448 679 KB

2

Görüntüdeki soruya bakalım:

Verilenler

  • f \cdot g(x) = x^4 - 1
  • g(x) = x - 1

Sorulan: f(1) kaçtır?

Çözüm

  1. Çarpımlı Fonksiyonun Bulunması:
    [
    f(x) \cdot (x - 1) = x^4 - 1
    ]

  2. x = 1 İçin Değer Bulma:
    [
    f(1) \cdot (1 - 1) = 1^4 - 1
    ]
    Burada soldaki ifade f(1) \cdot 0 olur, yani sonuç sıfırdır. Sağda ise 1 - 1 = 0.

    Bu durumda, hem 0 çarpanı olduğu için hem de işlem sonucu 0 olduğu için; buradan f(1) hakkında direkt bir bilgi elde edemeyiz.

  3. Farklı Değerleri Kullanma:
    Genel çözüm yolu olarak, diğer x değerleri üzerinden gidilerek f(x) fonksiyonunu belirleyebiliriz; ama burada bir özellikle dikkat edilmesi gereken not bulunuyor:
    [
    f(x) = \frac{x^4 - 1}{x - 1}
    ]

  4. Fonksiyonun Sadeleştirilmesi (Polinom Bölmesi):
    x^4 - 1, x-1 ile bölünebilir:
    [
    x^4 - 1 = (x-1)(x^3 + x^2 + x + 1)
    ]

    Sadeleştirme sonucu:
    [
    f(x) = x^3 + x^2 + x + 1
    ]

  5. f(1) Hesaplanması:
    [
    f(1) = 1^3 + 1^2 + 1 + 1 = 1 + 1 + 1 + 1 = 4
    ]

Bu durumda, f(1) = 4 olur.