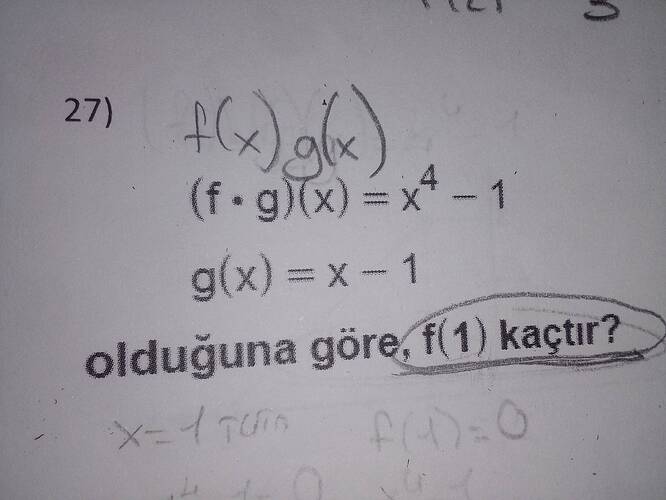Resimdeki soruya göre:
Verilenler:
[ (f \cdot g)(x) = x^4 - 1 ]
[ g(x) = x - 1 ]
Buna göre, ( f(1) ) kaçtır?
Çözüm:
Öncelikle bileşke fonksiyonun tanımını hatırlayalım:
[ (f \cdot g)(x) = f(x) \cdot g(x) ]
Verilen fonksiyonlar:
- ( (f \cdot g)(x) = x^4 - 1 )
- ( g(x) = x - 1 )
( f(x) \cdot g(x) = (x^4 - 1) ) olduğundan ve ( g(x) = x - 1 ), ( f(x) )'i bulmak için yerine koyarız:
[ f(x) \cdot (x - 1) = x^4 - 1 ]
x = 1 için bakarsak, bu denklemi ( f(1) \cdot (1 - 1) = 0 \cdot f(x) = x^4 - 1 ) ile çözmeye çalışırsak, görüyoruz ki:
[ 0 \cdot f(1) = 0 ]
Buradan ( f(1) ) değeri direkt anlaşılmadığından dolayı, ( x \neq 1 ) için çözmeye başvurmalıyız:
[ f(x) = \frac{x^4 - 1}{x - 1} ]
Bu ifadeyi sadeleştirmek için polinom bölmesi veya çarpanlara ayırma yapabiliriz. ( x^4 - 1 ) ifadesi, ( (x^2 - 1)(x^2 + 1) ) ve ( x^2 - 1 ) de ( (x - 1)(x + 1) ) şeklinde çarpanlarına ayrılır. Bu durumda:
[ \frac{(x - 1)(x + 1)(x^2 + 1)}{x - 1} ]
[ = (x + 1)(x^2 + 1) ]
Şimdi ( f(1) )'i bulabiliriz:
[ f(1) = (1 + 1)(1^2 + 1) ]
[ = 2 \cdot 2 ]
[ = 4 ]
Sonuç olarak, ( f(1) = 4 ) olacaktır.