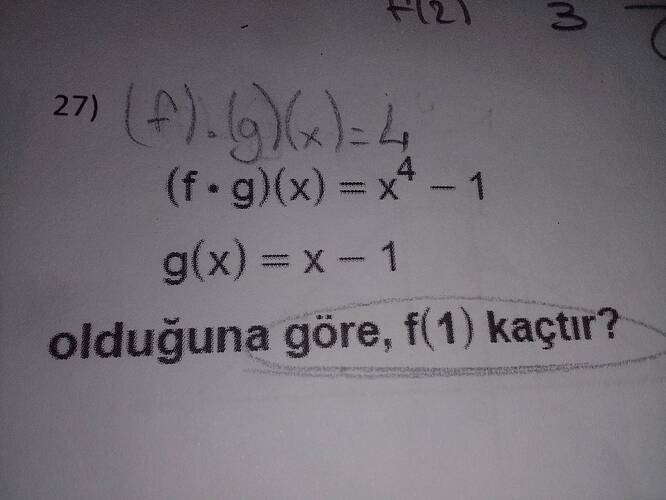Görüntüde bir matematik sorusu var. Soruda ( (f \cdot g)(x) = x^4 - 1 ) ifadesi ile ( g(x) = x - 1 ) veriliyor ve ( f(1) ) değeri soruluyor.
Öncelikle ( (f \cdot g)(x) = f(x) \cdot g(x) ) ifadesini açarak başlayalım. Verilenlere göre:
f(x) \cdot (x - 1) = x^4 - 1
Bu ifadeyi ( f(x) ) açısından çözmek için:
f(x) = \frac{x^4 - 1}{x - 1}
Şimdi ( x^4 - 1 ) ifadesini çarpanlarına ayıralım. Bu ifade, bir fark formudur:
x^4 - 1 = (x^2 + 1)(x^2 - 1)
Daha da çarpanlarına ayıralım:
x^4 - 1 = (x^2 + 1)(x - 1)(x + 1)
Bu durumda ( f(x) ) ifadesi:
f(x) = \frac{(x^2 + 1)(x - 1)(x + 1)}{x - 1}
Bu ifadede ( (x - 1) ) çarpanları sadeleşir:
f(x) = (x^2 + 1)(x + 1)
Şimdi ( f(1) ) değerini bulalım:
f(1) = (1^2 + 1)(1 + 1)
f(1) = (1 + 1)(2)
f(1) = 2 \cdot 2 = 4
Sonuç olarak, ( f(1) ) değeri 4’tür.