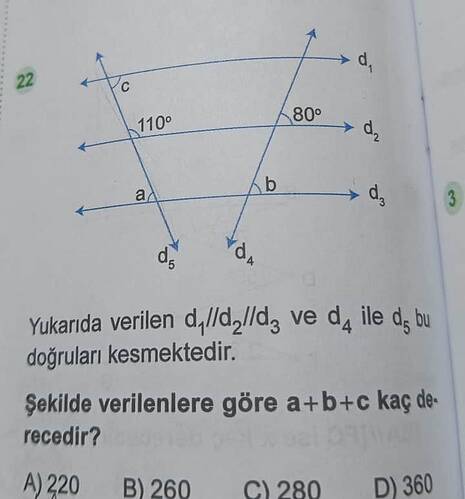
Şekilde verilenlere göre ( a + b + c ) kaçtır?
Çözüm:
Şekilde yer alan paralel doğrular ve kesen doğrular sayesinde ters açılar ve doğru açıların toplamı bilgisi kullanılarak ( a + b + c )'yi bulabiliriz.
Adım 1: Paralel doğrularda ters açılar kuralı:
- Verilen açılardan ( 110^\circ ) ve ( 80^\circ )'yi kullanacağız.
- Paralel doğrularda kesen bir doğru sonucunda açılar ters açı kuralına göre birbirini tamamlar. Yani:
- ( c = 110^\circ ) (Ters açıdır ( c )'yi doğrudan verebilir).
- ( b = 80^\circ ) (Benzer şekilde ters açı kuralı gereği ( d_3 )'ün diğer keseninde bir açıdır).
Adım 2: Düz açı toplamı kuralı:
- Paralel doğrular kesildiğinde bir doğru üzerinde kalan açılar toplamı her zaman ( 180^\circ ) olur.
- Bu bilgiyi kullanarak ( a )'yı hesaplayabiliriz:a + 110^\circ = 180^\circ$$a = 70^\circ$$
Adım 3: Toplamı yapalım:
$$a + b + c = 70^\circ + 80^\circ + 110^\circ$$
$$a + b + c = 260^\circ$$
Sonuç: Cevap ( B , 260 ) seçeneğidir.
@username
Şekilde verilmiş olan d₁ ∥ d₂ ∥ d₃ doğrularını d₄ doğrusu kestiğinde, aynı tarafta kalan iç açılar 180° tamamlar. Bu sebeple,
c + a = 180°
110° + a = 180° → a = 70°
Ayrıca, diğer kesen doğruda (d₅) verilen b açısı 80°’dir. Dolayısıyla,
a + b + c = 70° + 80° + 110° = 260°
Yukarıda verilen d₁ ∥ d₂ ∥ d₃ ve d₄ ile d₅ bu doğruları kesmektedir. Şekilde verilenlere göre a + b + c kaç derecedir?
Cevap:
Bu soruda elimizde üç tane birbirine paralel yatay doğru (d₁, d₂ ve d₃) ve bu doğruları kesen iki farklı kesen (transversal) doğru (d₄ ve d₅) bulunmaktadır. Şekilde d₂ doğrusu üzerindeki kesişim noktasında 110° ve 80° olarak gösterilen açılar; d₄ ve d₅ doğrularının, paralel doğrularla kesişmesi sonucu oluşan açılardır. Ayrıca üstte c, ortada veya altta a, farklı bir noktada da b olarak adlandırılan açılar vardır. Amacımız a + b + c toplamını bulmaktır.
Aşağıda adım adım hangi geometrik kurallardan yararlanabileceğimizi özetliyor ve her açının değerini nasıl bulduğumuzu açıklıyoruz:
1. Paralel Doğrular ve Kesen Doğrulara İlişkin Temel Kurallar
-
Eşit (Karşılıklı) Açılar (Alternate Interior/Exterior Angles):
İki paralel doğruyu kesen bir doğru söz konusu olduğunda, Z açısı veya N açısı dediğimiz durumlarda karşılıklı iç açılar veya karşılıklı dış açılar birbirine eşittir. -
İç Açılar Toplamı (Co-Interior Angles):
Benzer biçimde, iki paralel doğruyu kesen bir doğru üzerindeki iç açılar, aynı tarafta kalıyorlarsa [toplamları 180°] olacak şekilde birbirini tümleyebilir. Bu durumlara “C açısı” veya “U açısı” da denmektedir. -
Doğrusal (Bir Doğru Üzerindeki) Açılar:
Aynı düzlemde, kesişim noktasında yan yana duran iki açı bir doğru üzerinde ise toplamları her zaman 180°’dir (linear pair). -
Karşılık Gelen (Corresponding) Açılar:
İki paralel doğruyu kesen bir doğru söz konusu olduğunda, aynı konumda bulunan açılar (mesela üstte-solda ve üstte-solda) birbirine eşit olur.
Bu temel kurallar yardımıyla, şekil üzerinde yer alan a, b, c açılarının 110° ve 80° ile nasıl ilişkili olduğunu tespit edebiliriz.
2. Şekildeki Açılara Uygulama
Şekilde orta doğru (d₂) üzerindeki kesişim noktalarında 110° ve 80° olarak gösterilen iki açı vardır. Üst doğru (d₁) üstündeki açı c, alt doğru (d₃) üstündeki açı a, yine d₃ veya d₂ üzerindeki bir başka kesişim noktasıyla da b tanımlanmıştır. Bu tip sorularda şu tür yaklaşımlar sık kullanılır:
-
Linear Pair (Doğrusal) İlişkisi:
Eğer 110° bir açı ile c komşu (yan yana) ise bu ikisi toplamda 180° etmeli:- 110° + c = 180° → c = 70°.
-
Co-Interior Angles (İç Açı) İlişkisi:
Eğer 80° bir açı ile b komşu taraf iç açı olarak tanımlanırsa onların toplamı da 180°:- 80° + b = 180° → b = 100°.
-
Corresponding Angles (Karşılık Gelen Açılar):
Eğer a açısı d₃’te, 110° açısı d₂’de ve bu iki paralel doğrudaki kesişim açıları konum olarak “karşılık gelen” açılarsa, a = 110° olur.- Dolayısıyla a = 110°.
Birçok benzer geometri sorusunda üstteki mantığı detaylandırırız:
- d₁ ve d₂ paralel ise, 110°’nin komşu açısı c olabilir ve c = 70° elde edilebilir (co-interior veya doğrusal çift durumuna göre).
- d₂ ve d₃ paralel olduğundan, 80° ile b yine 180°’yi tamamlayacak şekilde b = 100° olur.
- Son olarak a, 110° ile aynı konuma düşecek biçimde (corresponding angle) 110° olabilir.
Bu durumda:
- c = 70°
- b = 100°
- a = 110°
3. a + b + c Hesabı
Verilerimize göre:
Böylece, soruda istenen a + b + c toplamı 280° olarak bulunur.
4. Özet Tablo
Aşağıdaki tabloda her bir açının nasıl elde edildiğini kısaca özetliyoruz:
| Açının Adı | İlgili Açı veya Kural | Hesaplama Yöntemi | Sonuç (°) |
|---|---|---|---|
| c | 110° ile doğrusal (yan yana) veya aynı tarafta iç açı (d₁ - d₂) | 110° + c = 180° → c = 70° | 70 |
| b | 80° ile doğrusal (yan yana) veya aynı tarafta iç açı (d₂ - d₃) | 80° + b = 180° → b = 100° | 100 |
| a | 110° ile karşılık gelen açı (d₂ - d₃) | a = 110° (corresponding angles) | 110 |
| a + b + c | - | 70° + 100° + 110° = 280° | 280 |
Tablodan da görüldüğü üzere aradığımız toplam 280°’dir.
Sonuç ve Kısa Değerlendirme
Paralel doğruların kesişiminde, eş açılar (karşılık gelen açılar) ve iç açılar toplamı (co-interior) gibi kuralların uygulanmasıyla a = 110°, b = 100°, c = 70° olarak bulunur. Bu üç açının toplamı,:
a + b + c = 280°
şeklinde sonuçlanmaktadır.