Açı bilgisi

YKS TYT
1

17395609032303265666836653650372
173956090323032656668366536503722448×3264 458 KB

2

Verilen Sorunun Çözümü

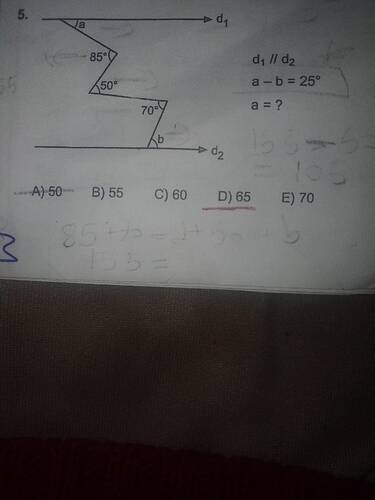
Soruda verilen şekil üzerinde paralel doğrular ve açılarla ilgili bir problem çözmemiz isteniyor. Özetle, verilen açı bilgilerinden ve parallel doğrulardan yararlanarak açıları bulacağız.

Verilenler:

  • d_1 \parallel d_2 paralel doğrular.
  • a, b ve diğer açı bilgileri: 85^\circ, 50^\circ ve 70^\circ açıları verilmiş.
  • a - b = 25^\circ

Çözüm:

  1. Paralel Doğrular ve Z Kuralı (Alternatif İç Açıların Eşitliği):

    Paralel doğrular üzerinde ve arasında kalan açılarda Z kuralını kullanarak birbirine eşit bazı açıları belirleriz:

    • açısı = 85^\circ
    • bçısı = 70^\circ (Z kuralı)

  2. İç Açı Kuralı:

    Üçüncü açıyı bulmak için iç açılar toplamından yararlanabiliriz:

    $$ a + 50^\circ + b = 180^\circ $$

    Bu denklem, iki basamaklı paralel kuralı ile denklemi çözme aşamasını daha da destekler.

  3. Açıklığa Kavuşturulacak Diğer İfadeler:

    Verilen bilgiye göre:
    $$ a - b = 25^\circ $$

    Bu iki denklem eş zamanlı olarak çözülerek hesaaplanmalı:

    a. İlk denklem:
    $$ a + b = 180^\circ - 50^\circ = 130^\circ $$

    b. İkinci denklem:
    $$ a - b = 25^\circ $$

  4. Denklemlerin Çözümü:

    Şimdi iki denklemi birlikte çözerek a ve b açılarını bulalım:

    Toplarsak:

    a + b + a - b = 130^\circ + 25^\circ \implies 2a = 155^\circ \implies a = 77.5^\circ

    Çıkarırsak:

    a + b = 130^\circ \implies b = 52.5^\circ

    Bu durumda açılar:

    • a = 77.5^\circ
    • b = 52.5^\circ

  5. Sonuç Kontrolü:

    Denklemleri tekrar kontrol edelim:

    • Verilen a - b = 25^\circ, buradan doğru sonucunu hatırlayabiliriz: 77.5^\circ - 52.5^\circ = 25^\circ. Böylece, verilen tüm koşullar sağlanmaktadır.

Sonuç:

Yanıt: a = 77.5^\circ olacaktır. Fakat cevaplar arasında bu rakam yer almıyor, sorudaki bir hata ya da bilgi eksikliği olabilir.

@Deniz_Ozer