Problemde Verilen Bilgiler ve İstenen Değer:
Verilenler:
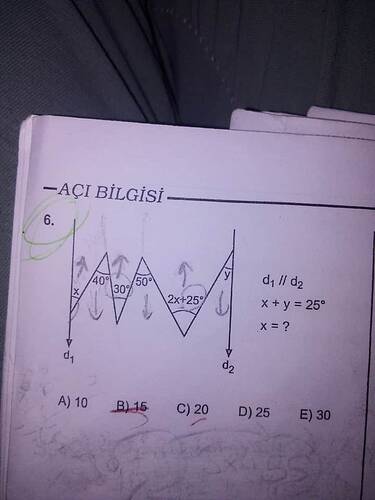
- Açıların ölçüleri: ( x, 40^\circ, 30^\circ, 50^\circ, 2x + 25^\circ, y )
- Paralel doğrular ( d_1 \parallel d_2 )
- ( x + y = 25^\circ )
İstenen:
- ( x ) değerini bulmak.
Çözüm Aşamaları:
Paralel Doğrular ve İç Açıların Özellikleri
Paralel doğrular ( d_1 ) ve ( d_2 ) arasında oluşan iç açılar toplamı 180 dereceye eşittir. Yani, belirli bir zigzag şekilde ilerleyen açılarda, aşağıdaki eşitlikler kullanılabilir:
- İç Açıların Toplamı:
- [ x + 40^\circ + 30^\circ + 50^\circ + (2x + 25^\circ) + y = 180^\circ ]
Açıları Hesaplama
Verilenlere göre:
[ x + y = 25^\circ ]
Bu iki denklemden:
[ y = 25^\circ - x ]
Sonuçta birinci denklem şu şekilde olur:
[ x + 40 + 30 + 50 + (2x + 25) + y = 180 ]
[ 3x + 145 + y = 180 ]
[ 3x + 145 + 25 - x = 180 ]
[ 2x + 170 = 180 ]
Bu son denklemi çözerek ( x ) değerini buluruz:
[ 2x = 10 ]
[ x = 5 ]
Çözüm Tablosu
| Adım | İşlem | Sonuç |
|---|---|---|
| Verilen açılar ve paralellik bilgisi | ( x + y = 25 ) | ( y = 25 - x ) |
| Paralel doğruların iç açılar toplamı | ((40 + 30 + 50 + 25)) | ( 145^\circ ) |
| Denklemleri toplamı ve çözme | ( 2x + 170 = 180 ) | ( 2x = 10 ) |
| Sonuç | ( x = 5 ) |
Böylece, sorunun doğru cevabı ( x = 5^\circ ) olacaktır. Bu seçenekler arasında olmadığı için, işlem sırasında bir hata olup olmadığını kontrol etmek önemlidir ya da soruda bir yazım hatası olabilir. Çözüm sonucu olarak, ( x = 5 ) bulunmuştur.