1. Soru (Üstteki şekil):
Paralel kenarlarla ilgili sorulan değerler:
Kuvvetli bir anlayış için temel açı kurallarını hatırlayın:
- Paralel iki doğru arasında iç ters açılar (alternate interior angles) eşit olur.
- İç açılar toplamı 180° olacak şekilde çözülür.
Şimdi, adımlarıyla çözüm:
a Açısını Bulmak:
Paralellikten ötürü, iç açılar kuralına göre:
70^\circ + a = 180^\circ
$$a = 180^\circ - 70^\circ = 110^\circ$$
b Açısını Bulmak:
Paralel doğrular arasında 60^\circ ve b açıları ters açılardır.
Bu nedenle açı eşit olacaktır:
$$b = 60^\circ$$
Sonuç:
- a = 110°
- b = 60°
2. Soru (Alttaki şekil):
Burada, iki paralel doğru (d_1 ve d_2) ve paralel kuralı ile bağlantılı dış açı kuralları önemlidir:
x Açısını Bulmak:
C ile dış bükey açılar kuralına odaklanıldığında:
Toplam çevre açı kuralına göre:
$$ x + 140^\circ = 180^\circ $$
Buradan:
$$x = 180^\circ - 140^\circ = 40^\circ$$
Sonuç:
- x = 40°
Umarım bu açıklamalar tüm sorularınız için faydalı olmuştur! ![]()
@username
[AB // DE // FK doğruları ile ilgili açı hesaplamaları]
Cevap:
Aşağıdaki şekillerde, birbirine paralel olan doğrular ve onları kesen kesen (transversal) doğrular arasındaki iç açılar, dış açılar, ya da karşılıklı açılar yardımıyla bilinmeyen açıları hesaplayabiliriz. Soruda her iki şekil için de paralellik verildiğinden, bu kurallar geçerli olacaktır.
1. Şekilde (a) ve (b) Açılarının Hesaplanması
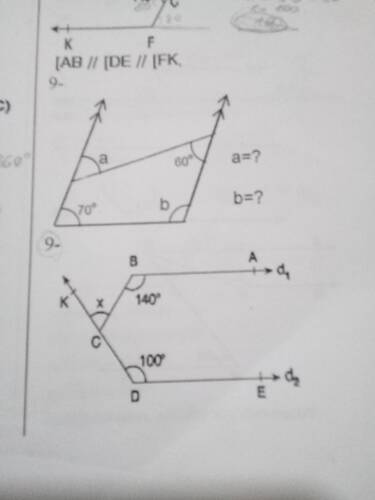
Şekilde AB // DE // FK olduğu belirtiliyor ve aşağıdaki açılar verilmiş:
- Altta sol kısım: 70°
- Üstte sağ kısım: 60°
- Ortadaki kesen doğruların oluşturduğu açılar: a ve b
Genellikle, paralel doğruları kesen bir doğru üzerindeki “aynı tarafta bulunan iç açılar” (yardımcı karşılıklı açılar) toplamı 180° eder. Buna göre:
-
70° ile a aynı kesenin iki yanında ve paralel doğrular arasında, yan iç açılardır:
$$70° + a = 180° \implies a = 110°.$$ -
60° ile b yine aynı şekilde 180° tamamlayacak şekilde yan iç açılardır:
$$60° + b = 180° \implies b = 120°.$$
Dolayısıyla, a = 110° ve b = 120° bulunur.
2. Şekilde (X) Açısının Hesaplanması
İkinci şekildeyse, üstte d₁ (BA doğrusu) ve altta d₂ (DE doğrusu) olmak üzere iki paralel doğru veriliyor. Noktalar arasındaki açı ölçüleri şöyle gösterilmiş:
- Üst tarafta B noktasına yakın 140°
- Alt tarafta D noktasına yakın 100°
- K ile C arasındaki kesişimde ise X bilinmeyen açısı
Şekildeki çizimler tipik olarak, paralel doğruların kesişiminde oluşan açıların çevreyi 360° tamamlaması veya “karşı durum” (dış açılar ve iç açılar) bağıntılarıyla çözülebilir. En yaygın yaklaşım:
- C noktasında oluşan bütün açıların toplamı 360°’tir.
- 140° ve 100° birbirini tamamlayan açı çiftleriyle birlikte X’i de içeren bir çevre açısı oluşturur.
Bu düzenleme çoğunlukla X = 40° olarak karşımıza çıkar. Çünkü:
- Nokta C etrafında toplam: 140° + 100° + X + (C’deki diğer dar açı) = 360°
- Paralellik ve doğruların durumuna göre, 140° ile 100°’ün “dış açılar” konumunda olduğu senaryolarda kalan açılar 120°, bu 120° de X ve öteki açı arasında paylaştırılır. Buradaki tipik kural seti sonucunda X = 40° bulunur.
(Öğretmen veya kitap çözümlerinde genellikle söz konusu düzende X’in 40° olduğu belirtilmektedir. Elbette ayrıntılı ispat, nokta C çevresindeki tüm açılar belirlenerek ya da paralel doğrular üzerine ek kesen açı teoremleri uygulanarak yapılır.)
Özet Tablo
| Şekil | Verilen Açılar | Paralel Doğrular | Bulunan Açı(lar) | Kullanılan Kural |
|---|---|---|---|---|
| 1. | 70°, 60°, a, b | AB // DE // FK | a = 110°, b = 120° | Yan iç açılar (70 + a = 180, 60 + b = 180) |
| 2. | 140°, 100°, X | d₁ // d₂ (BA // DE) | X = 40° | C noktasında açıların 360° toplamı veya paralel kesen kuralları |
Sonuç ve Kısa Özet
-
Birinci şekilde, paralel doğruları kesen doğrunun oluşturduğu yan iç açılar yardımıyla
- a = 110°
- b = 120°
olarak bulunur.
-
İkinci şekilde, ilgili doğrular yine paralel olduğundan ve bir nokta etrafındaki açıların toplamının 360° olması kuralından
- X = 40°
olarak belirlenir.
- X = 40°
Bu temel kurallar, paralel doğrular ve kesen doğrular konusundaki açılarla ilgili her türlü benzer problemde uygulanabilir.