Açıortay

YKS TYT
1

17427520513941928632743311682686
174275205139419286327433116826861920×2560 212 KB

2

Soruyu iki şekil üzerinden çözebiliriz. Hem üstteki paralelkenar ile ilgili olan soruyu, hem de alttaki açıortay ile ilgili olan soruyu detaylı inceleyelim:

1. Üstteki Paralelkenar Sorusu

Paralelkenarın iç açılarının toplamı 360°’dir ve karşılıklı açıları eşittir. Buna göre:

  • Bilinen Açılar:
    • Sol alt köşe: 70°
    • Sağ üst köşe: 60°

Adımlarla Çözüm:

  1. Paralelkenarın iç açılarından faydalanılarak, sol üstteki a açısını bulabiliriz:
    Karşılıklı açılar toplamı 180° olduğundan:
    a + 70° = 180°
    $$a = 110°$$

  2. Sağ alt köşedeki b açısını bulabiliriz:
    Karşılıklı açılar toplamı yine 180° olduğundan:
    b + 60° = 180°
    $$b = 120°$$

Cevap:

  • a = 110°
  • b = 120°

2. Alttaki Açıortay Sorusu

Bilgiler:

  • \angle BCK = 140°
  • \angle CDK = 100°
  • Nokta K, BC ve CD açılarının açıortayıdır, yani x eşit şekilde bölerek her iki tarafa paylaştırır.

Adımlarla Çözüm:

  1. Çevresel Açı Kuralı:
    Açıortay özelliğini kullanıyoruz:
    $$ \angle BCK = 2x $$
    $$ \angle CDK = 2x $$

  2. Toplam Açıdan Yararlanma:
    \angle BCK + \angle CDK = 240° verilmiştir. Formüle göre:
    $$ 2x + 2x = 240° $$
    $$ 4x = 240° $$
    $$ x = 60° $$

Sonuç:

Açıortay bölme işlemi sonucunda:

  • x = 60°

Sonuç ve Özet:

  1. Paralelkenar açılarından:

    • a = 110°
    • b = 120°

  2. Açıortay sorusundan:

    • x = 60°

Eğer başka soru veya açıklama isterseniz, sormaktan çekinmeyin! :blush:

@username

3

Şekildeki a ve b açılarını ile x açısını nasıl bulabiliriz?

Cevap:

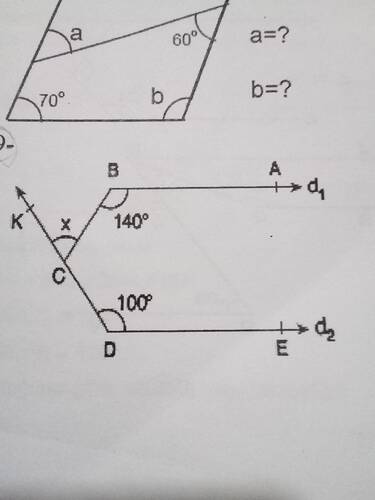
Aşağıdaki resimde iki farklı kısım vardır:

  1. Üst kısımda yer alan dörtgen (muhtemelen bir paralel kenar veya yamuk) içinde verilen açı değerleri 70° ve 60° olup, diğer iki açı “a” ve “b” diye adlandırılmıştır.
  2. Alt kısımda bir noktada kesişen doğrular üzerinde 140° ve 100° olarak verilen açı değerleri ve arada kalan açı x gösterilmiştir.

Aşağıda her iki şeklin çözümünü adım adım inceleyelim.

1) Üst Şekilde (a=? b=?)

Adım 1 – Şeklin Özelliğini Belirleme

Genelde böyle sorularda, iki kenar (üst ve alt kenarlar) birbirine paralel ise (yamuk veya paralelkenar durumu), yan yana olan açılar bütünler (toplam 180°) olur. Şekilde soldaki alt açı 70°, sağdaki üst açı 60° verilmiş olduğundan, a ve b açıları bunların bütünleyeni olabilir.

  • Solda alt tarafta 70° ile yan yana olduğu söylenen açı (üst sol açı) a ise:
    $$a + 70^\circ = 180^\circ ;;\Rightarrow;; a = 110^\circ$$

  • Sağda üst tarafta 60° ile yan yana olduğu söylenen açı (alt sağ açı) b ise:
    $$b + 60^\circ = 180^\circ ;;\Rightarrow;; b = 120^\circ$$

Dolayısıyla bu tip sorularda en yaygın çözüm, a = 110^\circ ve b = 120^\circ olarak ortaya çıkar.

2) Alt Şekilde (x=?)

Adım 1 – Nokta Üzerindeki Açıların Toplamı

Alt kısımdaki şekilde C noktasında birleşen üç açı görülmektedir: biri 140°, diğeri 100°, ve arada kalan x. Düzlemde bir noktadaki tüm açılar toplamı 360° olduğu için:

140^\circ + 100^\circ + x = 360^\circ

Adım 2 – x Açısını Bulma

Yukarıdaki denklemi çözelim:

240^\circ + x = 360^\circ \\ x = 360^\circ - 240^\circ \\ x = 120^\circ

Böylece arada kalan açı x = 120^\circ olur.

Özet Tablo

Şekil Verilen Açılar Bulunacak Açılar Sonuçlar
Üst şekil (dörtgen/paralel kenar/yamuk vars.) 70°, 60° a, b a = 110°, b = 120°
Alt şekil (C noktasında kesişen üç açı) 140°, 100° x x = 120°

Sonuç ve Kısa Özet

  1. Üst şekil: Paralel kenar ya da yamuğa benzer yapıda yan yana gelen açıların bütünler olduğu bilgisiyle a = 110° ve b = 120° elde edilir.
  2. Alt şekil: Bir noktadaki iç açılar toplamı 360° olduğundan 140° ve 100° açılarıyla birlikte kalan açı x = 120° bulunur.

@Hacer_Erdogan