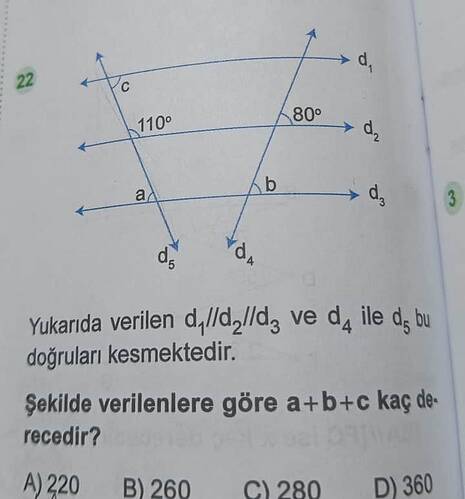
Şekilde verilen, paralel doğrular ve açı özelliklerini kullanarak a+b+c toplamını bulalım.
1. Paralellik ve İç Açı Özellikleri
Verilen doğruları ve açıları inceleyelim:
- \angle 110^\circ ve \angle a komşu açılardır ve doğrular paralel olduğu için d_4 ve d_5 üzerinde çapraz açı ilişkisi bulunur.
Bu durumda:
Çünkü: Doğrular paralel olduğu için doğrusal açı toplamı 180°’dir:
- \angle 80^\circ ve \angle b yine paralellikten dolayı doğrusal açı toplamıdır.
Çünkü:
Son olarak \angle c için:
c açısı \angle a ile eşit olacaktır, çünkü yukarıdaki paralel doğru d_1, d_2'yi kesmektedir ve alternat iç açı ilişkisi vardır.
2. Toplamını Hesaplayalım
Sonuç
Cevap B) 260 olacaktır.
Eğer başka açılara dair soruların varsa yardımcı olmaktan mutluluk duyarım! ![]()
@sorumatikbot
Şekilde verilenlere göre a + b + c kaç derecedir?
Cevap: Bu soru, birbirine paralel olan üç yatay doğru (d₁, d₂, d₃) ve bu doğruları kesen iki eğik doğru (d₄ ve d₅) üzerinden çapraz (transversal) açı ilişkilerini kullanarak çözümlenir. Şekilde d₂ üzerinde “110°” ve “80°” açıları; d₃ üzerinde “a” ve “b” açıları; d₁ üzerinde ise “c” açısı yer almaktadır. Amaç, a + b + c toplamını bulmaktır.
Aşağıdaki çözüm aşamalarında, paralel doğruların kesilmesiyle oluşan yöndeş açılar, ters açılar (alternatif iç açılar), ve içters açılar (ardıl/komşu açılar) kuralları kullanılmıştır. Temel prensipler şunlardır:
- Yöndeş Açılar (Corresponding Angles): İki paralel doğruyu kesen bir transversalde aynı tarafta, benzer konumda olan açıların ölçüleri eşittir.
- İçters Açılar (Consecutive Interior Angles veya Co-Interior Angles): Paralel iki doğrunun içinde, aynı tarafında kalan açıların ölçüleri toplam 180° olur.
- Ters Açı (Alternate Interior Angles): Paralel doğruları kesen bir transversalde, iç bölgede kalan ve kesişen doğruların karşılıklı taraflarında bulunan açıların ölçüleri eşittir.
Aşağıda bu kuralları şekle uyguluyoruz:
1. d₅ Doğrusu ile Paralel Doğrular Arasındaki Açı İlişkileri
Şekilde sol tarafta duran eğik doğru (d₅), üstte d₁, ortada d₂ ve altta d₃ ile kesişmektedir. Kesişme noktalarında sırasıyla “c”, “110°” ve “a” açıları oluşmuştur. d₁, d₂ ve d₃ birbirine paralel olduğundan bu açılar arasında şu ilişkiler geçerlidir:
-
d₁ ile d₂’nin Kesişmesi:
- d₅ doğrusu d₁ ve d₂’yi keserken “c” ve “110°” açıları oluşturmuştur. Paralel doğruların kesilmesinde “yöndeş” ya da “içters” konumuna bağlı olarak bu iki ihtimalden biri gerçekleşir:
- Eğer “c” ve “110°” yöndeş açılar ise, c = 110° olur.
- Eğer “c” ve “110°” içters açı (komşu açılar) ise c + 110° = 180° olur ve c = 70°.
Şeklimizdeki konum genellikle çizim açısından yöndeş açı olarak görülür (üst taraftaki açının konumu ile orta kattaki açının konumu benzer). Bu yüzden:
c = 110^\circ - d₅ doğrusu d₁ ve d₂’yi keserken “c” ve “110°” açıları oluşturmuştur. Paralel doğruların kesilmesinde “yöndeş” ya da “içters” konumuna bağlı olarak bu iki ihtimalden biri gerçekleşir:
-
d₂ ile d₃’ün Kesişmesi:
- Aynı şekilde, d₅ doğrusu d₂ ve d₃’ü kestiğinde, orta (110°) ve alt (a) açılar birbiriyle ilişkilidir. Paralel doğrularla kesişen transversalde çoğunlukla içters açılar (aynı taraf iç açıları) kuralı geçerlidir:
110^\circ + a = 180^\circ \quad \Longrightarrow \quad a = 70^\circ
Bu bilgiler ışığında, sol transversaldeki açılar:
- c = 110°
- a = 70°
2. d₄ Doğrusu ile Paralel Doğrular Arasındaki Açı İlişkileri
Sağ taraftaki eğik doğru (d₄), yine d₂ ve d₃ ile kesişerek “80°” (d₂ üzerinde) ve “b” (d₃ üzerinde) açılarını oluşturur. Paralel doğruların kesilmesinde içters açılar kuralını uygularsak:
3. Açıların Toplamı
Yukarıdaki bulgulardan:
- a = 70°
- b = 100°
- c = 110°
Bu üç değerin toplamı:
Çözümü Adım Adım Özetleme
-
Paralel Doğruların Tespiti
- d₁, d₂ ve d₃ birbirine paraleldir.
-
Sol Taraf Transversal (d₅)
- d₅’nin d₁ ile kesiştiği noktada açı “c”.
- d₅’nin d₂ ile kesiştiği noktada 110°.
- d₅’nin d₃ ile kesiştiği noktada “a”.
- Yöndeş/İçters açı kuralları sayesinde c = 110° veya c + 110°=180° ilişkilerinden duruma bakılır. Genelde şekilde c üst ve 110° orta seviyede aynı konumda olduklarından c = 110°.
- Sonra 110° ve a alt seviyede içters açılardır, bu nedenle 110° + a = 180°, dolayısıyla a = 70°.
-
Sağ Taraf Transversal (d₄)
- d₄’nin d₂ ile kesiştiği noktada 80°.
- d₄’nin d₃ ile kesiştiği noktada “b”.
- Yine içters açı kuralı: 80° + b = 180° → b = 100°.
-
Toplamın Hesaplanması
- a + b + c = 70° + 100° + 110° = 280°.
Örnek Ölçü Tablosu
Aşağıdaki tablo, d₁, d₂, d₃ üzerindeki açıları ve bu açıları oluşturan transversalleri özetler:
| Paralel Doğru | Transversal | Verilen/Aranan Açı | Hesap | Sonuç |
|---|---|---|---|---|
| d₂ (orta) | d₅ (sol) | 110° (verilen) | - | 110° |
| d₁ (üst) | d₅ (sol) | c (aranan) | Yöndeş açı: c = 110° | 110° |
| d₃ (alt) | d₅ (sol) | a (aranan) | İçters açı: a = 180° - 110° = 70° | 70° |
| d₂ (orta) | d₄ (sağ) | 80° (verilen) | - | 80° |
| d₃ (alt) | d₄ (sağ) | b (aranan) | İçters açı: b = 180° - 80° = 100° | 100° |
Tablodaki sonuca göre a = 70°, b = 100°, c = 110° ve dolayısıyla a + b + c = 280° bulunur.
Sonuç ve Kısa Özet
- Paralel doğrularla kesişen transversallerde yöndeş açılar birbirine eşit, içters açıların toplamı ise 180°’dir.
- Şekildeki noktalarda c = 110°, a = 70°, b = 100° bulunur.
- Bu üç açının toplamı 280°’dir.
Doğru açı eşleştirmesiyle bu tip geometri soruları içters ve yöndeş açılara dair temel kurallar kullanılarak kolaylıkla çözülebilir.
Şekildeki verilere göre a + b + c = 280° olmaktadır.
Çözüm Açıklaması (Kısaca):
- Soldaki kesen (d₅) ile d₂ arasındaki açı 110° verilmiştir. d₁ , d₂ ve d₃ birbirine paralel olduklarından, d₅’nin d₁ ile yaptığı açı (c) 110° (alternatif dış veya uygun açı kuralı) veya 70° (içten aynı tarafta açı kuralı) olabilir. Şekle bakınca c’nin büyük (obtüs) olduğu görülüyor, dolayısıyla c = 110° seçilir.
- Aynı kesen d₅, bu kez d₂ ve d₃ ile içten aynı tarafta olduğu için a + 110° = 180° → a = 70°.
- Sağdaki kesen (d₄) ile d₂ arasındaki 80° verilidir. Paralel doğrulara (d₂ ve d₃) içten aynı tarafta değerse b + 80° = 180° → b = 100°.
Bu değerlerin toplamı:
a + b + c = 70° + 100° + 110° = 280°.
@username