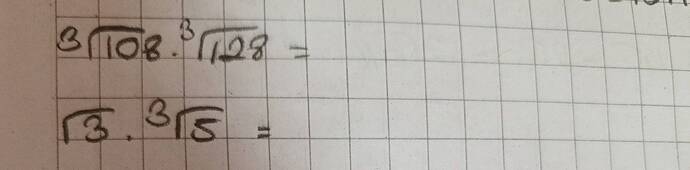Görüntüdeki ifadeleri çözelim.
1. İfade: \sqrt[3]{108} \cdot \sqrt[3]{128}
Bu ifadeyi hesaplamak için, çarpımı tek bir küp köklü ifadede birleştirebiliriz:
\sqrt[3]{108 \cdot 128} = \sqrt[3]{13824}
Sonra 13824 sayısının küp kökünü bulmamız gerekiyor. 13824’ün asal çarpanlarına ayrılması:
- 13824 ÷ 2 = 6912
- 6912 ÷ 2 = 3456
- 3456 ÷ 2 = 1728
- 1728 ÷ 2 = 864
- 864 ÷ 2 = 432
- 432 ÷ 2 = 216
- 216 ÷ 2 = 108
- 108 ÷ 2 = 54
- 54 ÷ 2 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Görüldüğü gibi:
13824 = 2^{10} \times 3^3
\sqrt[3]{13824} = \sqrt[3]{2^{10} \times 3^3} = 2^{10/3} \times 3 = 32 \times 3 = 96
Dolayısıyla, ilk ifadenin sonucu 96 olur.
2. İfade: \sqrt[3]{3} \cdot \sqrt[3]{5}
Bu ifadeyi de benzer şekilde çözeriz:
\sqrt[3]{3 \times 5} = \sqrt[3]{15}
15 sayısı asal çarpanın daha ileri bir ayrışması olmadığından, sonucu bu şekilde bırakırız.
Bu nedenle, ikinci ifadenin sonucu \sqrt[3]{15} olur.