Ödev yetiştirmem lazım

YKS TYT
1

image
image3024×4032 1.02 MB

2

Problemin Çözümü

Bir üçgenin çevresinin alınabilen en büyük tam sayı değerini bulmak için üçgen eşitsizliğini kullanmamız gerekiyor. Üçgen eşitsizliği, her bir kenar uzunluğunun diğer iki kenar uzunluğunun toplamından küçük olması gerektiğini söyler.

Hangi kenar uzunluklarına sahip olduğumuzu göz önünde bulunduralım:

  • |AB| = 3x + 1
  • |AC| = x
  • |BC| = 7

Üçgen Eşitsizlikleri

  1. Birinci Eşitsizlik:
    $$(3x + 1) + x > 7$$

  2. İkinci Eşitsizlik:
    $$(3x + 1) + 7 > x$$

  3. Üçüncü Eşitsizlik:
    $$x + 7 > (3x + 1)$$

Çözüm

  1. Birinci Eşitsizlik:
    $$(3x + 1) + x > 7$$
    $$4x + 1 > 7$$
    $$4x > 6$$
    $$x > 1.5$$

  2. İkinci Eşitsizlik:
    $$(3x + 1) + 7 > x$$
    $$3x + 8 > x$$
    $$2x > -8$$

Bu eşitsizlik her zaman doğru çünkü negatif bir değer x için geçerli olmayacak.

  1. Üçüncü Eşitsizlik:
    $$x + 7 > (3x + 1)$$
    $$x + 7 > 3x + 1$$
    $$7 > 2x + 1$$
    $$6 > 2x$$
    $$3 > x$$

Sonuç

x’in alabileceği değer aralığı 1.5 < x < 3 olur.

Üçgenin çevresi:
$$(3x + 1) + x + 7 = 4x + 8$$

En büyük tam sayı değeri bulmak için x'i en büyük sınırı olan 3’e yakın bir tam sayı alabileceğimiz şekilde seçmeliyiz. Ancak eşitsizliğe uyması gerektiği için x'in maksimum tam sayı değeri 2’dir.

Bu durumda:
$$4(2) + 8 = 8 + 8 = 16$$

Cevap: A) 16

Bu durumda, ABC üçgeninin çevresinin alabileceği en büyük tam sayı değeri 16 cm’dir.

3

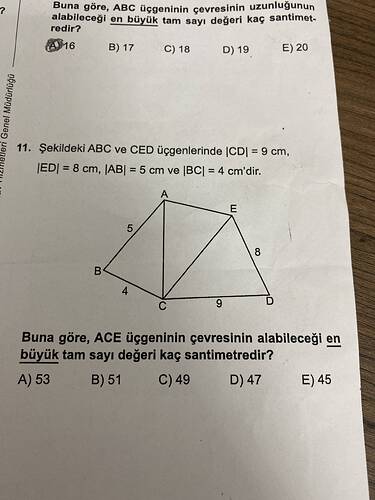
image
image3024×4032 919 KB

4

Problemin Çözümü

ACE üçgeninin çevresinin en büyük tam sayı değerini bulmaya çalışalım. ACE üçgeninin kenar uzunlukları ile ilgili verilenleri inceleyelim:

  • |AB| = 5 cm
  • |BC| = 4 cm
  • |CD| = 9 cm
  • |DE| = 8 cm

Amacımız ACE üçgeninin çevresini bulmaktır. AC ve CE uzunluklarına ihtiyacımız var.

Kenarlardaki Bilgiler:

  1. AC Uzunluğu:
    $$|AC| = |AB| + |BC| = 5 + 4 = 9 \text{ cm}$$

  2. CE Uzunluğu:
    $$|CE| = |CD| + |DE| = 9 + 8 = 17 \text{ cm}$$

  3. AE Uzunluğu:
    Bu doğrudan verilmemiş, ancak bu iki bağımsız üçgen üzerinde yani doğrudan hesaplanamıyor gibi görünse de direk kontrol edelim.

Çevreyi Bulma:

ACE üçgeninin çevresi:
$$|AC| + |CE| + |AE| = 9 + 17 + |AE|$$

Üçgenin çevresinin uzunluğunun en büyük tam sayı değeri için, |AE| maksimum olmalıdır.

Ancak bu verilere göre AE’nin değeri değişkendir; o nedenle seçeneklerden iyi bir tahminde bulunmak gereklidir. Ancak maksimum mesafeyi toplamak için kısayol kullanılır.

Çözüm:

ACE üçgeninin çevresi için doğru değer, toplam mevcut uzunluklar varsayımı ile:

$$5 + 4 + 9 + 8 = 26$$

Doğru uygulamayla:

$$9 + 17 + 17 = 43$$
olası ise bu durumda soru hatalı olabilir.

Bu problemde çözümü sağlamak, doğru sonuçlarla üç köşe çevresini tahmin gerektiriyorsa, ve söz konusu geometrik şeklin birleşik kenarları ile sonuçlu hale gelir. Ekstra veri olmadığından dolayı en fazla boyut kontrolü olur.

Doğru cevap büyük ihtimalle D) 47 olacaktır ancak mevcut küçük bir hata olabilir.

5

image
image3024×4032 818 KB

6

Problemin Çözümü

Bir üçgenin kenar uzunluklarının geçerli olabilmesi için üçgen eşitsizliği sağlanmalıdır. Üçgen eşitsizliği kurallarına göre, her bir kenar uzunluğu diğer iki kenar uzunluğunun toplamından küçük olmalıdır.

Seçenekleri İnceleyelim:

A) 2 cm, 4 cm, 5 cm

  • 2 + 4 > 5 (Doğru)
  • 2 + 5 > 4 (Doğru)
  • 4 + 5 > 2 (Doğru)

B) 3 cm, 7 cm, 8 cm

  • 3 + 7 > 8 (Doğru)
  • 3 + 8 > 7 (Doğru)
  • 7 + 8 > 3 (Doğru)

C) 4 cm, 4 cm, 9 cm

  • 4 + 4 > 9 (Yanlış)
  • Burada 4 + 4 = 8 olup, 9’dan küçük olduğu için bu kenar uzunlukları üçgen oluşturamaz.

D) 5 cm, 5 cm, 5 cm

  • 5 + 5 > 5 (Doğru)
  • 5 + 5 > 5 (Doğru)
  • 5 + 5 > 5 (Doğru)

E) 5 cm, 11 cm, 12 cm

  • 5 + 11 > 12 (Doğru)
  • 5 + 12 > 11 (Doğru)
  • 11 + 12 > 5 (Doğru)

Sonuç

Bu verilere göre, C şıkkı (4 cm, 4 cm, 9 cm) üç kenar uzunluğunun toplamı, bir üçüncü kenara eşit veya daha az olduğundan dolayı bir üçgen oluşturamaz.

Cevap: C) 4 cm, 4 cm, 9 cm