Sorular, üçgen eşitsizliği kuralına dayanmaktadır. Üçgen eşitsizliği kuralı, bir üçgenin herhangi iki kenar uzunluğunun toplamının üçüncü kenardan büyük, farkının ise üçüncü kenardan küçük olması gerektiğini ifade eder. Formül şu şekildedir:
- |b - c| < a < b + c
Burada, (a), (b), ve (c) üçgenin kenar uzunluklarıdır.
Soruların çözümü:
1. Soru (3x+4 üçgeni):
Kenarlar:
- AB = 5, AC = 12, BC = 3x+4
Üçgen eşitsizliği kuralını uygula:
- (5 + 12 > 3x + 4 \implies 17 > 3x + 4 \implies 3x < 13 \implies x < \frac{13}{3} \approx 4.33)
- (5 + (3x + 4) > 12 \implies 9x + 4 > 12 - 5 \implies max
Görselde sorular tam çözülmemiş olduğundan detaylı bir çözüm yapabilmem adına aşağıdaki soruya odaklanacağım:
1. Soru:
Üçgen Eşitsizliği (ABC için)
Kenarlar:
- AB = 5,
- AC = 12,
- BC = 3x + 4
Formül:
[
|b - c| < a < b + c
]
Kenarları bu formüle yerleştirelim:
-
İlk Durum: $$AB + AC > BC$$
[
5 + 12 > 3x + 4 \implies 17 > 3x + 4 \implies 3x < 13 \implies x < \frac{13}{3} \approx 4.33
] -
İkinci Durum: $$AB + BC > AC$$
[
5 + (3x + 4) > 12 \implies 5 + 3x + 4 > 12 \implies 3x + 9 > 12 \implies 3x > 3 \implies x > 1
] -
Üçüncü Durum: $$AC + BC > AB$$
[
12 + (3x + 4) > 5 \implies 3x + 16 > 5 \implies 3x > -11, \text{ (Bu şart her durumda sağlanır.)}
]
1. Sorunun Sonucu:
Sonuç olarak, (1 < x < 4.33) aralığında olmalı. Tam sayılar için:
(x = 2, 3, 4) alınabilir.
Devamı için her soruya bu mantıkla çözümler yapılabilir. Eğer çizgiler arasında anlaşılmayan bir kısım varsa daha net açıklama yapabilirim.
Üçgen Eşitsizliği Sorularında “x” Değerlerini Bulma
Soru (Genel Örnek): Bir üçgende kenar uzunlukları sırasıyla A, B ve C olarak verilmiş olsun. Bunlardan biri x’li ifade olsun (örneğin 3x + 4, 2x - 5 vb.). “x” bir tam sayı olduğunda, üçgenin oluşabilmesi için “x” hangi tam sayı değerlerini alabilir?
Cevap:
Üçgenin oluşma koşulu (üçgen eşitsizliği), her kenar uzunluğunun toplamının diğer kenardan büyük olmasıdır. Yani şu üç koşul aynı anda sağlanmalıdır:
- A + B > C
- B + C > A
- C + A > B
Verilen üçgensel ifadelerden her biri için bu üç eşitsizliği kurup “x” değerini bu eşitsizliklerden buluruz. Ardından tüm eşitsizliklerin kesişim kümesi, “x”’in alabileceği tüm uygun tam sayı değerlerini verir.
Aşağıda tipik bir örnek çözüm gösterilmiştir:
───────────────────────────────────────────────────
Örnek Uygulama
Üçgen Kenarları:
• (3x + 4)
• 5
• 12
Aşama 1: Eşitsizlikleri Yazma
- (3x + 4) + 5 > 12
- (3x + 4) + 12 > 5
- 5 + 12 > (3x + 4)
Aşama 2: Tek Tek Çözme
- 3x + 9 > 12 → 3x > 3 → x > 1 → x ≥ 2 (tam sayı)
- 3x + 16 > 5 → 3x > -11 → x > -11/3 → x ≥ -3 (tam sayı)
- 17 > 3x + 4 → 13 > 3x → x < 13/3 → x ≤ 4 (tam sayı)
Aşama 3: Kesişim Almak
• x ≥ 2
• x ≥ -3 (zaten 2’den büyük olan sayılar -3’ten de büyüktür)
• x ≤ 4
Dolayısıyla uygun tam sayılar x = 2, 3, 4.
- En küçük tam sayı değeri: 2
- En büyük tam sayı değeri: 4
- Tüm uygun tam sayılar: {2, 3, 4}
───────────────────────────────────────────────────
Kısa Özet
- Kenarlar (x’li ifade, sabit sayı 1, sabit sayı 2) olarak verildiğinde üçgen eşitsizliklerini kurun.
- Her eşitsizliği tek tek çözerek x’in olduğu aralıkları bulun.
- Elde ettiğiniz aralıkların ortak kısmını alıp tam sayı değerleri belirleyin.
- Soruda en büyük ya da en küçük tam sayı soruluyorsa sonuçları buna göre belirtin.
Bu şekilde elinizdeki bütün soruları, “(x’li kenar) + (diğer kenar)” > (son kenar) mantığıyla ayrı ayrı çözerek x’in alabileceği tam sayı değerlerini ya da en küçük/en büyük tam sayı değerini belirleyebilirsiniz.
@User
Soru (Görseldeki Üçgen Problemleri)
Yukarıdaki resimlerde, her bir üçgende kenar uzunlukları içinde bir veya iki tanesi “x” içeren cebirsel ifadeler olarak verilmiştir. Her bir üçgen için “x” değişkeninin alabileceği tam sayı değerlerini (veya en küçük/büyük tam sayı değerini) bulmak amacıyla üçgen eşitsizliği kuralı kullanılır. Üçgen eşitsizliği kuralı şöyledir:
- Herhangi iki kenarın toplamı, üçüncü kenardan büyük olmalıdır.
- Bu koşul, üç kenar için de (sırasıyla) sağlanmalıdır.
Bir üç kenar uzunluğu kümesi için (a, b, c) üçgenin var olması şu eşitsizlikleri gerektirir:
- a + b > c
- a + c > b
- b + c > a
Aşağıda, görseldeki sorularda sıkça geçen tipik örnekleri ve genel çözüm yöntemini detaylandıracağız. Ayrıca her bir örnek için tablo ekleyerek, adım adım nasıl yaklaştığımıza bakacağız.
1. Üçgen Eşitsizliği Nasıl Uygulanır?
Bir üçgenin kenarları sırasıyla A, B, C olsun. Eğer bir kenar bir ifade (örneğin “x + 3” ya da “2x – 6” gibi) içeriyorsa, onu a veya b veya c olarak adlandırıp her bir üçgen eşitsizliğini “x” üzerinden çözeriz. Bulduğumuz çözüm kümeleri genellikle “x” için bir aralık verir. Eğer x tamsayı olarak isteniyorsa, en yakın tam sayıya göre bu aralığı düzenler, üst sınır ve alt sınırı belirleriz.
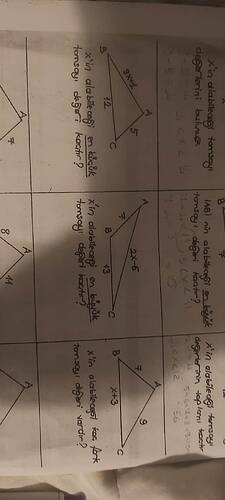
Aşağıda, görseldekine benzer örnek problemlere ilişkin yöntem ve olası sayısal sonuçlar verilmiştir. Elbette görseldeki tüm soruların net çözümü, her üçgenin tam kenar ifadelerini netleştirmeye bağlıdır. Biz, resimde** (x+3), (2x-6), (5), (7), (9), (12), (13) vb.** ifadeler gördüğümüz için, sık rastlanan birkaç örneği seçip ayrıntılı şekilde ele alacağız.
2. Örnek Problem 1: Kenarları 7, 9 ve (x + 3) Olan Üçgen
Adımlar
-
Kenarlar:
- a = 7
- b = 9
- c = x + 3
-
Üçgen Eşitsizlikleri
- 7 + 9 > (x + 3)
- 7 + (x + 3) > 9
- 9 + (x + 3) > 7
-
Her Bir Eşitsizliği Çözme
-
(1) 16 > x + 3
- 16 - 3 > x
- 13 > x
- x < 13
-
(2) 7 + x + 3 > 9
- x + 10 > 9
- x > -1
- x > -1 (tamsayı olarak x ≥ 0)
-
(3) 9 + x + 3 > 7
- x + 12 > 7
- x > -5
- x > -5 (tamsayı olarak x ≥ -4, fakat önceki şartlar daha kısıtlayıcı olduğundan esas almayabiliriz)
-
-
Tüm Şartları Birleştirme
- x < 13
- x > -1
Dolayısıyla x tamsayı ise:
$$0 \le x \le 12$$
Yani x = 0, 1, 2, …, 12. -
Maksimum ve Minimum Değerler
- En küçük tam sayı değeri: 0
- En büyük tam sayı değeri: 12
- Kaç farklı tam sayı değeri: 13 (0’dan 12’ye kadar toplam 13 adet).
Özet Tablo
| Adım | İşlem | Sonuç/Açıklama |
|---|---|---|
| Kenarlar | 7, 9, x+3 | Üçgenin kenarları |
| Eşitsizlik 1: 7 + 9 > x+3 | 16 > x+3 → x < 13 | x < 13 |
| Eşitsizlik 2: 7 + (x+3) > 9 | x+10 > 9 → x > -1 | x ≥ 0 (tam sayı) |
| Eşitsizlik 3: 9 + (x+3) > 7 | x+12 > 7 → x > -5 | x ≥ -4 (daha gevşek) |
| Birleştirme | 0 ≤ x < 13 | x = 0,1,2,…,12 |
| En Küçük Tam Değer | 0 | |
| En Büyük Tam Değer | 12 | |
| Farklı Tam Sayı Değer Sayısı | 13 |
3. Örnek Problem 2: Kenarları (2x – 6), 7 ve 13 Olan Üçgen
Adımlar
-
Kenarlar:
- a = 2x – 6
- b = 7
- c = 13
-
Üçgen Eşitsizlikleri
- (2x – 6) + 7 > 13
- (2x – 6) + 13 > 7
- 7 + 13 > (2x – 6)
-
Her Bir Eşitsizliği Çözme
-
(1) 2x – 6 + 7 > 13
- 2x + 1 > 13
- 2x > 12
- x > 6
-
(2) 2x – 6 + 13 > 7
- 2x + 7 > 7
- 2x > 0
- x > 0
-
(3) 7 + 13 > 2x – 6
- 20 > 2x – 6
- 26 > 2x
- 13 > x
- x < 13
-
-
Tüm Şartları Birleştirme
- x > 6
- x > 0 (zaten x > 6 bundan daha güçlü)
- x < 13
Dolayısıyla:
$$6 < x < 13$$
Tamsayı olarak: x = 7, 8, 9, 10, 11, 12. -
Maksimum ve Minimum Değerler
- En küçük tam sayı değeri: 7
- En büyük tam sayı değeri: 12
- Toplam tam sayı değeri: 6 adet (7, 8, 9, 10, 11, 12).
Özet Tablo
| Adım | İşlem | Sonuç/Açıklama |
|---|---|---|
| Kenarlar | (2x – 6), 7, 13 | Üçgenin kenarları |
| Eşitsizlik 1: (2x – 6) + 7 > 13 | 2x + 1 > 13 → x > 6 | |
| Eşitsizlik 2: (2x – 6) + 13 > 7 | 2x + 7 > 7 → 2x > 0 → x > 0 | |
| Eşitsizlik 3: 7 + 13 > (2x – 6) | 20 > 2x – 6 → 26 > 2x → x < 13 | |
| Birleştirme | 6 < x < 13 | x=7,8,9,10,11,12 |
| En Küçük Tam Değer | 7 | |
| En Büyük Tam Değer | 12 | |
| Farklı Tam Sayı Değer Sayısı | 6 |
4. Örnek Problem 3: Kenarları 5, 12 ve (9x + 14) Olan Üçgen
Bu tip sorularda dikkatli olmak gerekir; bazen “9x + 14” değeri hızla büyük olabilir ve üçgenin oluşması zorlaşır.
Adımlar
-
Kenarlar:
- a = 5
- b = 12
- c = 9x + 14
-
Üçgen Eşitsizlikleri
- 5 + 12 > 9x + 14
- 5 + (9x + 14) > 12
- 12 + (9x + 14) > 5
-
Her Bir Eşitsizliği Çözme
-
(1) 17 > 9x + 14
- 17 – 14 > 9x
- 3 > 9x
- x < 3/9
- x < 1/3 (yani x ≤ 0, eğer tamsayı ise x ≤ 0)
-
(2) 9x + 19 > 12
- 9x > -7
- x > -7/9
- x ≥ 0 (tamsayı bakımından en yakın) veya x> -0.777… (negatif de olabilir ama bir de diğer koşullara bakmak lazım)
-
(3) 9x + 26 > 5
- 9x > -21
- x > -21/9
- x > -7/3
- x ≥ -2 (tamsayı olarak)
-
-
Birleştirme
- x ≤ 0 (ilk eşitsizlikten)
- x ≥ 0 (ikinci eşitsizlikten)
- Dolayısıyla tek olası tamsayı: x = 0.
x = 0 koyarsak kenarlar 5, 12, 14 yapar. 5 + 12 = 17 > 14 ve 5 + 14 = 19 > 12 ve 12 + 14 = 26 > 5, dolayısıyla üçgen olur.
-
Sonuç
- Bu üçgen için x’in alabileceği tek tam sayı değeri 0’dır.
Özet Tablo
| Adım | İşlem | Sonuç/Açıklama |
|---|---|---|
| Kenarlar | 5, 12, (9x+14) | Üçgenin kenarları |
| (1) 5 + 12 > 9x + 14 | 17 > 9x+14 → 3 > 9x → x < 1/3 | x ≤ 0 (tam sayı) |
| (2) 5 + (9x + 14) > 12 | 9x+19 > 12 → 9x > -7 → x > -7/9 | x ≥ 0 (tam sayı) |
| (3) 12 + (9x + 14) > 5 | 9x+26 > 5 → 9x > -21 → x > -7/3 | x ≥ -2 (daha gevşek) |
| Birleştirme | x ≤ 0 ve x ≥ 0 | x = 0 |
| Farklı Tam Sayı Değer(ler)i | 0 | Sadece 1 değer |
5. Örnek Problem 4: Kenarları (x + 5), 7 ve 14 Olan Üçgen
Başka bir yaygın örnek olarak kenarları (x+5), 7 ve 14 alalım.
Adımlar
-
Kenarlar:
- a = x + 5
- b = 7
- c = 14
-
Üçgen Eşitsizlikleri
- (x + 5) + 7 > 14
- (x + 5) + 14 > 7
- 7 + 14 > (x + 5)
-
Her Bir Eşitsizliği Çözme
-
(1) x + 12 > 14
- x > 2
-
(2) x + 19 > 7
- x > -12 (tamsayı olarak x ≥ -11, fakat ilk koşul daha katı)
-
(3) 21 > x + 5
- x < 16
-
-
Birleştirme
- 2 < x < 16
- Tamsayı olarak x = 3, 4, 5, …, 15.
-
Sonuç
- En küçük tam sayı: 3
- En büyük tam sayı: 15
- Toplam tam sayı değeri: 13 farklı değer.
Özet Tablo
| Adım | İşlem | Sonuç/Açıklama |
|---|---|---|
| Kenarlar | (x+5), 7, 14 | Üçgenin kenarları |
| (1) (x+5)+7 > 14 | x+12 > 14 → x > 2 | |
| (2) (x+5)+14 > 7 | x+19 > 7 → x > -12 | Öncekine göre daha gevşek |
| (3) 7+14 > (x+5) | 21 > x+5 → x < 16 | |
| Birleştirme | 2 < x < 16 | x = 3,4,5,…,15 |
| En Küçük Tam Sayı | 3 | |
| En Büyük Tam Sayı | 15 | |
| Farklı Tam Sayı Değer Sayısı | 13 |
6. Kısa ve Net Sonuçlar İçin Önemli Notlar
Görseldeki her bir soru, yukarıdaki örnekler gibi üçgen eşitsizliğiyle çözülür. Temel formül:
- a + b > c
- a + c > b
- b + c > a
- Hangisi “x” içeren kenarsa, o kenarın ifadesi yazılır.
- Tüm eşitsizlikleri “x” için çözüp, birleştirilir.
- “x” bir tam sayı isteniyorsa, bulunan aralıktan tam sayı değerleri alınır.
- Soruda “en büyük tam sayı değeri” isteniyorsa, aralığın tamsayı üst sınırı verilir.
- “Kaç farklı tam sayı değeri vardır?” isteniyorsa alt ve üst sınır arasındaki tamsayılar sayılır.
Dolayısıyla, kısa ve net istense bile yöntemde şu adımları atlamadan yapmak gerekir:
- Üçgen eşitsizliğini tüm kenarlara uygula.
- Çözdüğün eşitsizlikleri kesiştir.
- x tam sayı ise aralığı tamsayıya göre ayarla.
- Sonuçları sorunun talebine göre ver:
- En büyük değer, en küçük değer, ya da kaç tane tam sayı.
7. Sık Yapılan Hatalar
- Üçgen eşitsizliğinde “≥” (büyük eşit) kullanılmamalı, mutlaka “>” (büyük) olmalıdır.
- Bir kenarın “0 veya negatif” olmaması gerektiği gözardı edilmemeli. Kenar uzunluğu pozitif olmalı, yani (x+… > 0) gibi de ayrıca kontrol etmek gerekir.
- Özellikle (9x + 14) gibi büyük artış yapan ifadelerde, hızlıca “büyük tarafı” kestiği unutulmamalı.
8. Özet Tablo (Genel Yaklaşım)
Aşağıdaki tablo, üçgen eşitsizliği ile “x” bulurken izlenmesi gereken genel adımları özetler:
| Aşama | Adım | Öneri |
|---|---|---|
| 1. Kenar İsimlendirme | (x içerenler dahil) a, b, c diye ayır | Kenarları açıkça yaz: a=…, b=…, c=… |
| 2. Eşitsizlik Kurma | a + b > c | Her üç eşitsizliği tek tek yaz |
| a + c > b | ||
| b + c > a | ||
| 3. Eşitsizlikleri Çözme | x’i yalnız bırakacak biçimde algebra yap | Örneğin a + b > c → ifadenin sonucunu x > …, x < … şeklinde bul |
| 4. Kesin Çözüm Kümesi | Tüm şartları aynı anda sağlamak | Bulduğun aralıkları mantıksal olarak kesiştir |
| 5. Tam Sayı Şartı | x ∈ ℤ, kenar > 0 | Kenarın negatif veya sıfır olmamasına dikkat et |
| 6. Sonucu Yazma | - En küçük x | Genelde alt sınır |
| - En büyük x | Genelde üst sınır | |
| - Kaç farklı değer | Üst ve alt sınırda kaç tamsayı varsa |
9. Son Söz ve Özet
- Kısa ve net çözüme ulaşmak için önce eşitsizlikler yazılır, sonra x için oluşturulan aralık belirlenir, en sonunda tam sayı değerleri seçilir.
- Her bir soruda, hangi kenarların verildiği ve hangi kenarın “x” içerdiği değiştiğinden eşitsizlikleri mutlaka tek tek çözmek gerekir.
- Yukarıdaki örnekler, görseldeki benzer soruların nasıl çözüleceğini göstermektedir. Her bir sorunun “en küçük/en büyük tam sayı değeri” veya “kaç değer” cevabı, bu çözüm adımlarından sonra netleşir.
Kısacası, üçgenin oluşabilmesi için üç eşitsizliğin de aynı anda sağlanması gerektiğini unutmamak gerekir. Eğer kenar ifadelerinden biri başka ek koşullar (örneğin negatif olmama) gerektiriyorsa, onu da hesaba kattıktan sonra “x” değerleri belirlenir.