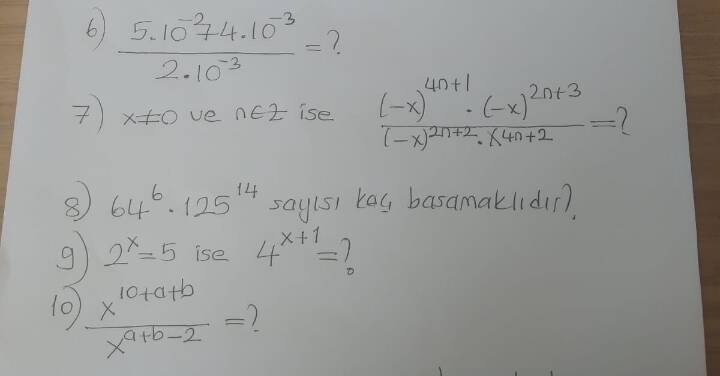Odevdeki Sorular ve Çözümleri
6) ( \frac{5 \cdot 10^2 \cdot 4 \cdot 10^{-3}}{2 \cdot 10^{-3}} = ? )
Çözüm:
-
Sayıları Birleştirme:
[
\frac{5 \cdot 4 \cdot 10^2 \cdot 10^{-3}}{2 \cdot 10^{-3}}
] -
Sadeleştirme ve Hesaplama:
[
\frac{20 \cdot 10^{-1}}{2 \cdot 10^{-3}} = \frac{20}{2} \cdot 10^{-1+3} = 10 \cdot 10^2
] -
Sonuç:
[
10^3 = 1000
]
Bu nedenle cevap (1000) olacaktır.
7) ( x \neq 0 ) ve ( n \in \mathbb{Z} ) ise ( \frac{(-x)^{4n+1} \cdot (-x)^{2n+3}}{(-x)^{2n+2} \cdot (-x)^{4n+2}} = ? )
Çözüm:
-
Üsleri Birleştirme:
[
\frac{(-x)^{4n+1 + 2n+3}}{(-x)^{2n+2 + 4n+2}} = \frac{(-x)^{6n+4}}{(-x)^{6n+4}}
] -
Sonuç:
[
(-x)^0 = 1
]
Cevap (1) olacaktır.
8) ( 64^6 \cdot 125^{14} ) sayısı kaç basamaklıdır?
Çözüm:
-
Tabanı Aynı Hale Getirme:
[
64 = 2^6 \quad \text{ve} \quad 125 = 5^3
] -
Dönüştürme:
[
(2^6)^6 \cdot (5^3)^{14} = 2^{36} \cdot 5^{42}
] -
Basamak Bulma:
[
2^{36} \cdot 5^{42} = 10^{36} \cdot 5^6 = 10^{36} \cdot 15625
][
\log_{10}(10^{36} \cdot 15625) = 36 + \log_{10}(15625)
][
\log_{10}(15625) = 4.1938 \implies \text{yaklaşık } 40.1938
]Sayı yaklaşık 41 basamaklıdır.
9) ( 2^x = 5 ) ise ( 4^{x+1} = ? )
Çözüm:
-
Tabanları Dönüştürme:
[
4^{x+1} = (2^2)^{x+1} = 2^{2x+2}
] -
İfade Dönüştürme:
[
2^{2x+2} = 2^2 \cdot 2^{2x} = 4 \cdot (2^x)^2
] -
Bilinenle Yerine Koyma:
[
4 \cdot 5^2 = 4 \cdot 25 = 100
]
Cevap (100) olacaktır.