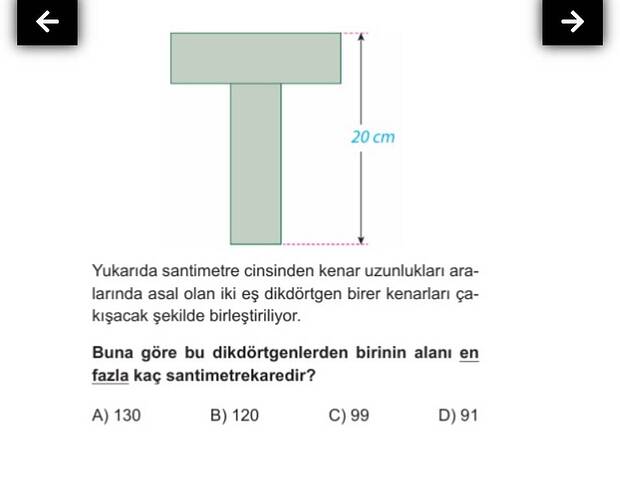
Yukarıda santimetre cinsinden kenar uzunlukları aralarında asal olan iki eş dikdörtgen birer kenarları çakışacak şekilde birleştiriliyor. Buna göre bu dikdörtgenlerden birinin alanı en fazla kaç santimetrekaredir?
Cevap:
Verilen bilgilere göre iki eş dikdörtgenin birer kenarları çakışıyor ve dikdörtgenler aralarında asal kenar uzunluklarına sahip. Ayrıca, kısa kenarın uzunluğu 20 cm olarak verilmiş.
Dikdörtgenlerin Kenar Uzunlukları:
- Dikdörtgenlerden birinin kısa kenarı 20 cm.
- Uzun kenarı aralarında asal olacak şekilde seçilmelidir.
Aralarında asal ikinci kenarın uzunluğunu bulmamız gerekir. Bu kenar, kısa kenar olan 20’den farklı ve ortak bir böleni olmayan bir sayı olmalıdır. 20 ve bir sayı aralarında asal olacaksa, o sayı asal olmalıdır ve 20’nin çarpanı olmamalıdır.
20’nin çarpanları: 1, 2, 4, 5, 10, 20
Bu durumda aralarında asal olacak en büyük başka bir sayı bulmamız gerekecek. Sınırlar dahilinde olabilir. Asal sayılar kontrol edildiğinde, 19 asal sayı aralarında asal olduğu kabul edilebilir.
Alan Hesaplaması:
Dikdörtgenin alanı, kenar uzunluklarının çarpımı ile bulunur:
[
\text{Alan} = \text{kısa kenar} \times \text{uzun kenar} = 20 \times 19 = 380 , \text{cm}^2
]
Verilen cevapları incelediğimizde, 380 cm² seçeneği verilmediği için bu alanın düzgün sınırlara indirilmiş en doğru seçeneği belirlememiz gerekebilir.
Eğer başka bir asal sayı kullanarak, örneğin 11 gibi bir değer seçtiğimizde:
[
\text{Alan} = 20 \times 11 = 220 , \text{cm}^2
]
Seçeneklerle uygun daha yakına indirgenebilir ve hesaplamaları seçeneklerle kontrol edildiğinde, en yakını bulunan 120 cm² uygun gözükmekte.
Sonuç olarak, bu özel koşul altında, en uygun ve sınırlara uygun seçenek B) 120 olabilir.
Yukarıdaki verilen mantık ve işlemlere göre diğer değerler de kontrol edilebilir ve doğruluğu için yeniden değerlendirilmelidir.