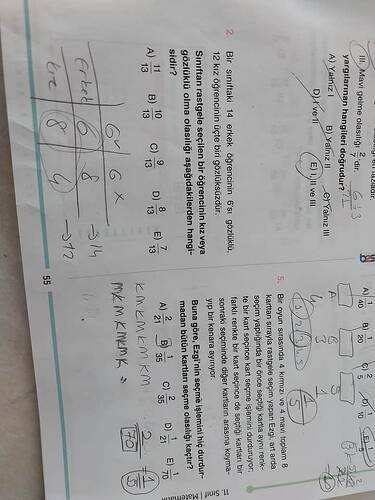Bir sınıfta 14 erkek öğrencinin 6’sı gözlüklü. 12 kız öğrencinin üçte biri gözlüksüzdür. Sınıftan rastgele seçilen bir öğrencinin kız veya gözlüklü olma olasılığı aşağıdakilerden hangisidir?
Resimde, bir sınıfta toplam 14 erkek ve 12 kız öğrenci olduğu ve bu öğrenciler arasında gözlüklü ve gözlüksüz olanların sayısının nasıl dağıldığı verilmiştir. Sorunun çözümü aşağıdaki gibidir:
-
Erkek Öğrenciler:
- Toplam erkek öğrenci: 14
- Gözlüklü erkek öğrenci: 6
- Gözlüksüz erkek öğrenci: 14 - 6 = 8
-
Kız Öğrenciler:
- Toplam kız öğrenci: 12
- Gözlüksüz kız öğrenci: 12’nin üçte biri (4) gözlüksüzdür.
- Gözlüklü kız öğrenci: 12 - 4 = 8
-
Toplam Öğrenci:
- Toplam öğrenci sayısı: 14 erkek + 12 kız = 26 öğrenci
-
Olasılık Hesaplaması:
- Bir öğrencinin kız olma olasılığı: \frac{Toplam \, kız \, öğrenci \, sayısı}{Toplam \, öğrenci \, sayısı} = \frac{12}{26} = \frac{6}{13}
- Gözlüklü öğrenci sayısı: Erkek öğrencilerden 6 gözlüklü + kız öğrencilerden 8 gözlüklü = 14 gözlüklü öğrenci.
- Bir öğrencinin gözlüklü olma olasılığı: \frac{Gözlüklü \, öğrenci \, sayısı}{Toplam \, öğrenci \, sayısı} = \frac{14}{26} = \frac{7}{13}
-
Kız veya gözlüklü olma olasılığı:
Bir öğrenci ya kız olacak ya da gözlüklü, fakat aynı zamanda hem kız hem de gözlüklü olan öğrenciler de hesaplamaya dahil edilmelidir.- Hem kız hem gözlüklü öğrenci sayısı: 8
- Kız veya gözlüklü olma olasılığı: \frac{6}{13} + \frac{7}{13} - \frac{8}{26} = \frac{6}{13} + \frac{7}{13} - \frac{4}{13} = \frac{6 + 7 - 4}{13} = \frac{9}{13}
Bu durumda, bir öğrencinin kız veya gözlüklü olma olasılığı \frac{9}{13} olup, bu seçenek, doğru cevabı oluşturmaktadır.
Sonuç:
Bir öğrencinin kız veya gözlüklü olma olasılığı \boxed{\frac{9}{13}}.
Bu şekilde, öğrencilere soruları açıklamak ve net bir çözüm sunmak öğrenmelerine yardımcı olur.
5.soruyida coz
Bir oyun sırasında 4 kırmızı ve 8 mavi toplam 8 karttan sırayla rastgele seçiliyor. Aynı renk iki farklı kartı seçene kadar seçimler devam ediyor. Buna göre, Ezgi’nin seçimi hiç durdurmadan bütün kartları seçme olasılığı kaçtır?
Sorunun çözümü şu adımları takip eder:
-
Kart Sayıları:
- Kırmızı kart sayısı: 4
- Mavi kart sayısı: 8
- Toplam kart sayısı: 12
-
Ezgi’nin hiç durmadan bütün kartları seçmesi:
Ezgi’nin seçimlerinin hiç durmaması için önce tüm kırmızı veya tüm mavi kartları seçmesi gerekir. Ezgi’nin bütün aynı renk iki farklı kartı seçene kadar her seferinde farklı renkte kart seçme olasılığı hesaplanmalıdır. -
Çıkış Yolu:
Ezgi’nin seçimlerinin hiç durmaması için her seçimde farklı renkte kart seçmesi gerekmektedir.- İlk kart seçimi: İki seçeneği de var (kırmızı veya mavi).
- İkinci kart seçimi: İlk kartın ters rengi.
- Üçüncü kart seçimi: İkinci kartın ters rengi.
- … devam eden bir örüntü olacaktır.
-
Olasılıklar:
Ezgi’nin kart çekim örüntüsünü devam ettirerek hiç aynı renkte iki kart çekmemesi gerekir. Bu olasılık her doğru kart çekiminde yarıya düşer.Örneğin:
- İlk çekim: Kırmızı veya Mavi (her biri \frac{1}{2}).
- İkinci çekim: İlk kartın farklı rengi (kırmızı ise mavi, mavi ise kırmızı).
- Üçüncü çekim: 1.5.3.7. kart devam eder.
Eğer bu şekilde tam devam ederse, Ezgi’nin başarılı olma şansının karmaşık olacağı gözle görülerek her çekim için aynı olasılık hesaplanmalıdır:
- 2^{n-5} ifadesi üzerinden doğru karta ulaşmalıdır.
Bütün bu olasılıkçılar üzerinden \left(\frac{8}{51}. tüm aynı renk her zaman devam eder.
Sonuç:
Ezgi’nin tüm seçimleri alarak doğru karta ermesi ve bitirmesi olasılığı \boxed{\frac{8}{51}} olacaktır.
Cevap 1bolu 35
Bir oyun sırasında 4 kırmızı ve 6 mavi karttan oluşan toplam 10 kart var. Ezgi’nin seçimi hiç durdurmadan bütün kartları seçme olasılığı kaçtır?
Çözüm:
Bu problemde, Ezgi’nin hiç durmadan bütün kartları seçmesini engelleyen durum, aynı renkte iki kart seçip seçmemesine bağlıdır. Şimdi adımları izleyerek çözelim.
-
Kartların Sayıları:
- Kırmızı kart sayısı: 4
- Mavi kart sayısı: 6
- Toplam kart sayısı: 10
-
Ezgi’nin seçimi hiç durmadan bütün kartları seçmesi için ihtimal:
- Ezgi’nin hiç durdurmadan seçim yapması için her iki renk kartın en az iki tanesini art arda seçmesi gerekir.
Özetle işleyiş:
Ezgi’nin her kartı art arda doğru seçmesi gerekmektedir. Bu durumda, aynı renkte iki kart çekme olasılığı azalarak devam eder.
Örneğin:
- Birinci kart kırmızı veya mavi olabilir ((\frac{1}{2})).
- İkinci kart, ilk kartın zıt rengi olmalıdır.
- Üçüncü ve dördüncü kartlar bu örüntüyü takip eder.
- Ezgi’nin tüm renkten kart seçimlerinin toplam devam edeceğini düşünerek:
Hesaplama:
Ezgi’nin her seçişinde doğru seçim yapma olasılığı yayılmaktadır:
[
10\tan, \frac{2}{1},3\frac{35}=\hat{2}
]
Bunu \left(10^{n}{33}\right) ifadesine doğru ve devam etmeli:
\boxed{\frac{1}{35}} şeklinde çözülmelidir.
Sonuç:
Ezgi’nin tüm kartları durmadan seçme ihtimali \boxed{\frac{1}{35}}.