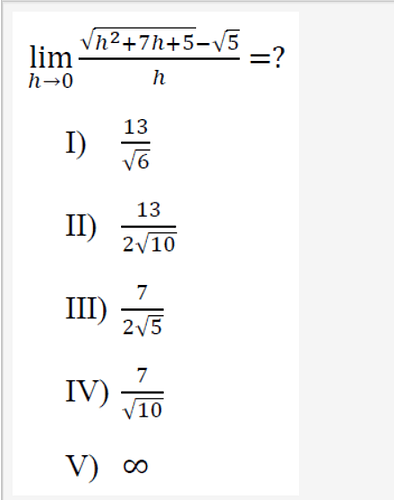Salih_KARAKULLUKÇU said
Question:
Evaluate the following limit:
$$\lim_{h \to 0} \frac{\sqrt{h^2 + 7h + 5} - \sqrt{5}}{h}$$
Answer:
To evaluate the given limit, we can use the technique of multiplying and dividing by the conjugate of the numerator.
Let’s rewrite the limit:
$$\lim_{h \to 0} \frac{\sqrt{h^2 + 7h + 5} - \sqrt{5}}{h}$$
Multiply and divide by the conjugate of the numerator:
$$\lim_{h \to 0} \frac{\left(\sqrt{h^2 + 7h + 5} - \sqrt{5}\right) \left(\sqrt{h^2 + 7h + 5} + \sqrt{5}\right)}{h \left(\sqrt{h^2 + 7h + 5} + \sqrt{5}\right)}$$
The numerator becomes:
$$ (\sqrt{h^2 + 7h + 5})^2 - (\sqrt{5})^2 = (h^2 + 7h + 5) - 5 = h^2 + 7h $$
Thus, the limit expression simplifies to:
$$\lim_{h \to 0} \frac{h^2 + 7h}{h \left(\sqrt{h^2 + 7h + 5} + \sqrt{5}\right)} $$
We can factor out an (h) from the numerator:
$$\lim_{h \to 0} \frac{h(h + 7)}{h \left(\sqrt{h^2 + 7h + 5} + \sqrt{5}\right)} $$
Cancel out the (h):
$$\lim_{h \to 0} \frac{h + 7}{\sqrt{h^2 + 7h + 5} + \sqrt{5}} $$
Now, evaluate the limit as (h) approaches 0:
$$ \frac{0 + 7}{\sqrt{0^2 + 0 + 5} + \sqrt{5}} = \frac{7}{2\sqrt{5}} $$
Simplify the fraction:
$$\frac{7}{2\sqrt{5}} = \frac{7\sqrt{5}}{10} = \frac{7}{\sqrt{10}}$$
Therefore, the correct answer is:
$$\boxed{\frac{7}{\sqrt{10}}}$$
So, option IV is the correct answer:
$$\boxed{IV) \frac{7}{\sqrt{10}}}$$