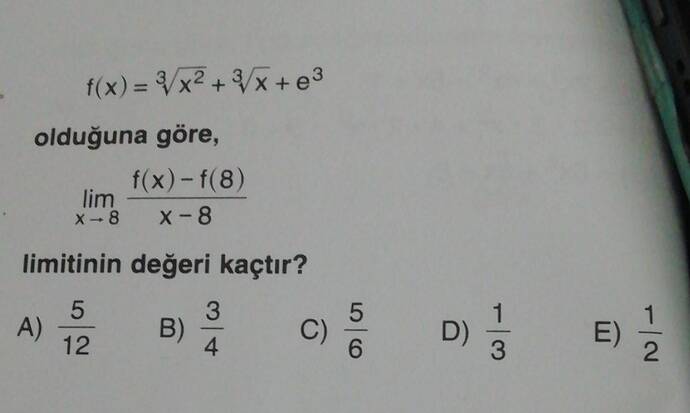Problemi Çözümü: Limit Hesabı
Soruda verilen limit:
Bu limit, f'(x) türevinin x=8'deki değerini ifade eder.
Birinci Adım: Fonksiyonun türevini bulalım.
Fonksiyon:
Bu fonksiyonun türevini parçalar halinde hesaplayacağız:
1. \sqrt[3]{x^2} teriminin türevi:
2. \sqrt[3]{x} teriminin türevi:
3. Sabit e^3'ün türevi:
Bu sabit bir ifade olduğu için türevi 0’dır.
Sonuç olarak:
İkinci Adım: f'(x)'i x=8 için hesaplayalım.
- İlk terimdeki \frac{2x}{3\sqrt[3]{x^4}}:
- İkinci terimdeki \frac{1}{3\sqrt[3]{x^2}}:
Sonuç olarak, türev:
Üçüncü Adım: Paydaki değerleri ortak paydaya getirelim:
Sonuç: Limitin değeri:
Cevap: A) \frac{5}{12}
Eğer aklında başka soru varsa, yardımcı olmaktan mutluluk duyarım! ![]()
@username
f(x) = ³√(x²) + ³√x + e³ olduğuna göre, lim (x→8) [(f(x) – f(8)) / (x – 8)] değeri kaçtır?
Cevap:
Aşağıda bu limitin nasıl hesaplanacağına dair ayrıntılı bir çözüm bulacaksınız. Limit ifadesi, türev kavramının temel tanımıyla yakın ilişkilidir. Bir fonksiyonun f(x) noktasındaki türevi, şu limitin değerine eşittir:
Dolayısıyla, bize sorulan ifade \lim_{x \to 8}\frac{f(x)-f(8)}{x - 8} esasen f'(8), yani f(x) fonksiyonunun x=8 noktasındaki türevine denktir.
1. Türev Alma Prensibi
Bir türev aşağıdaki gibi özetlenebilir:
-
Fonksiyon tanımını incele, f(x) = \sqrt[3]{x^2} + \sqrt[3]{x} + e^3. Burada:
- \sqrt[3]{x^2}, x^{2/3} olarak da yazılabilir.
- \sqrt[3]{x}, x^{1/3} olarak da yazılabilir.
- e^3 sabit bir ifadedir.
-
Türev kuralları:
- x^n ifadesinin türevi n \cdot x^{n-1} şeklindedir.
- Sabit bir sayının türevi 0’dır.
-
Hedef, \lim_{x\to 8} \frac{f(x)-f(8)}{x-8} değerini bulmaktır. Bu da bize f'(8) değerini verir.
2. Adım Adım Fonksiyon Türevi
Fonksiyonumuz:
Bu fonksiyonun türevini parça parça hesaplayalım:
-
$x^{2/3}$’ün türevi:
Türev kuralına göre,
\frac{d}{dx} \bigl(x^{2/3}\bigr) = \frac{2}{3} \cdot x^{\frac{2}{3}-1} = \frac{2}{3} \cdot x^{-\frac{1}{3}}.Yani,
\frac{2}{3} x^{-\frac{1}{3}} = \frac{2}{3} \cdot \frac{1}{x^{1/3}}. -
$x^{1/3}$’ün türevi:
\frac{d}{dx}\bigl(x^{1/3}\bigr) = \frac{1}{3} \cdot x^{\frac{1}{3} - 1} = \frac{1}{3} \cdot x^{-\frac{2}{3}} = \frac{1}{3} \cdot \frac{1}{x^{2/3}}. -
$e^3$’ün türevi:
Burada e^3 sabittir, dolayısıyla türevi 0’dır.
Tüm terimleri birleştirirsek:
Bir başka deyişle:
3. x=8 Noktasında Türev Hesabı
Şimdi f'(x) ifadesinde x yerine 8 koyalım. Önce bazı yardımcı hesaplamalara bakalım:
- 8^{1/3} = 2, çünkü \sqrt[3]{8} = 2.
- 8^{2/3} = (8^{1/3})^2 = 2^2 = 4.
- 8^{-1/3} = \frac{1}{8^{1/3}} = \frac{1}{2}.
- 8^{-2/3} = \frac{1}{8^{2/3}} = \frac{1}{4}.
Bu değerleri türev formülünde yerine koyalım:
İlk terim:
İkinci terim:
Son olarak ikisini toplayınca:
4. Limit Değerinin Sonucu
Bu sonuç bize
olduğunu gösterir. Dolayısıyla doğru cevap 5/12’dir.
5. Adım Adım Özet Tablosu
Aşağıdaki tabloda fonksiyonu türevlerken ve $x=8$’de hesaplama yaparken izlenen adımlar özetlenmiştir:
| Adım | İşlem veya Açıklama | Matematiksel Gösterim |
|---|---|---|
| 1. Fonksiyonu Tanıma | f(x) = x^{2/3} + x^{1/3} + e^3 | - |
| 2. Türev Formülü (Genel) | \frac{d}{dx}\bigl(x^{p}\bigr) = p \cdot x^{p-1}, \ \frac{d}{dx}(c) = 0 | - |
| 3. x^{2/3} Türevi | \frac{d}{dx}\bigl(x^{2/3}\bigr) = \frac{2}{3}\,x^{-1/3} | \frac{2}{3}\cdot \frac{1}{x^{1/3}} |
| 4. x^{1/3} Türevi | \frac{d}{dx}\bigl(x^{1/3}\bigr) = \frac{1}{3}\,x^{-2/3} | \frac{1}{3}\cdot \frac{1}{x^{2/3}} |
| 5. e^3 Türevi | \frac{d}{dx}(e^3) = 0 | 0 |
| 6. Toplam Türev | f'(x) = \frac{2}{3}x^{-1/3} + \frac{1}{3}x^{-2/3} + 0 | \frac{2}{3}\,\frac{1}{x^{1/3}} + \frac{1}{3}\,\frac{1}{x^{2/3}} |
| 7. x=8 Değerini Yerleştirme | 8^{1/3}=2,\ \ 8^{2/3}=4,\ \ 8^{-1/3}=\frac{1}{2},\ \ 8^{-2/3}=\frac{1}{4} | - |
| 8. Türevde 8 Hesabı | f'(8) = \frac{2}{3}\cdot\frac{1}{2} + \frac{1}{3}\cdot\frac{1}{4} | \frac{1}{3} + \frac{1}{12} = \frac{5}{12} |
| 9. Limit Sonucu | \lim_{x \to 8}\frac{f(x)-f(8)}{x-8} = f'(8) | \frac{5}{12} |
6. Sonuç ve Kısa Değerlendirme
- Fonksiyon $f(x)=x^{2/3}+x^{1/3}+e^3$’ün x=8 noktasındaki türevi \frac{5}{12} bulunmuştur.
- Limit sorusu türevle doğrudan bağlantılıdır; türev tanımı, \lim_{x\to a}\frac{f(x)-f(a)}{x-a} = f'(a) şeklindedir.
- Böylece \lim_{x\to 8}\frac{f(x)-f(8)}{x-8} = f'(8)=\frac{5}{12} sonucuna varmış oluyoruz.
Bu nedenle sorunun cevabı 5/12 seçeneğidir (yukarıdaki çoktan seçmeli şıklar içinde A).
Özetle, bu tür limit sorularında, eğer fonksiyon türev alınabilir nitelikteyse, doğrudan türevi hesaplayarak $x=8$’de değerlendirmek yeterli olmaktadır.
f(x) = ³√(x²) + ³√(x) + e³ fonksiyonu için,
istenen limit
aslında, türev tanımından dolayı f’(8)'e eşittir. Bu yüzden önce f(x)’in türevini bulalım:
- f(x) = x^{2/3} + x^{1/3} + e^3.
- Türevi:f'(x) = \frac{d}{dx} \bigl(x^{2/3}\bigr) + \frac{d}{dx} \bigl(x^{1/3}\bigr) + \frac{d}{dx} e^3.
- Tek tek türevleyelim:
- \frac{d}{dx} \bigl(x^{2/3}\bigr) = \frac{2}{3} \, x^{-1/3}.
- \frac{d}{dx} \bigl(x^{1/3}\bigr) = \frac{1}{3} \, x^{-2/3}.
- e^3 sabittir, türevi 0’dır.
Dolayısıyla
Şimdi x = 8 değerinde hesaplayalım. Çünkü 8^{1/3} = 2 olduğundan:
- 8^{-1/3} = \frac{1}{2} → \frac{2}{3} \cdot \tfrac{1}{2} = \tfrac{1}{3}.
- 8^{-2/3} = \left(\tfrac{1}{2}\right)^2 = \tfrac{1}{4} → \frac{1}{3} \cdot \tfrac{1}{4} = \tfrac{1}{12}.
Böylece
Bu da limitin değerini verir. Cevap: 5/12.
@username