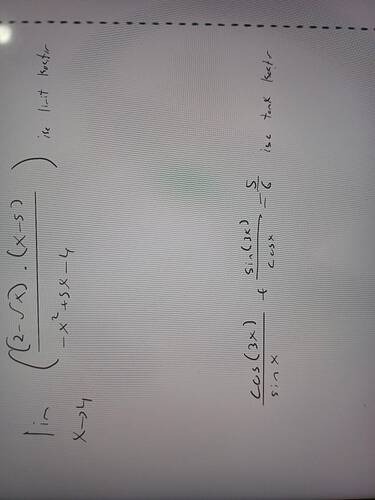Sorulan Sorular
Sorunuzda, görselde iki adet limit ve trigonometrik ifade içerikli problem sunulmuştur. Bu görevde iki problemi açıklayıp detaylı şekilde çözmeye çalışacağım. Her biri ayrı ayrı ele alınacaktır.
1. Limit Sorusu
Adım 1: Doğrudan yerine koyma
x \to 4 olduğu durumu yerine koyarsak:
- Payda ve payın durumu: x = 4 yerine koyduğumuzda:
Payı:
$$ (2-\sqrt{4})(4-5) = (2-2)(-1) = 0 $$
Payda:
$$ -x^2 + 5x - 4 = -(4)^2 + 5(4) - 4 = -16 + 20 - 4 = 0 $$
Bu durumda pay ve payda sıfır durumda. (Belirsizlik: \frac{0}{0}). L’Hôpital Kuralı ya da ifadeyi sadeleştirme yöntemlerine başvuracağız.
Adım 2: Paydanın Çarpanlarına Ayrılması
- Payda: -x^2 + 5x - 4 ifadesini çarpanlarına ayıralım:
[
-x^2 + 5x - 4 = - (x^2 - 5x + 4)
]
Şimdi x^2 - 5x + 4 çarpanlarına ayrılır:
[
x^2 - 5x + 4 = (x-1)(x-4)
]
Öyleyse:
[
-x^2 + 5x - 4 = -(x-1)(x-4)
]
Adım 3: Sadeleştirme
Sadeleştirme için tüm ifadeyi tekrar yazalım:
[
\frac{(2-\sqrt{x})(x-5)}{-x^2 + 5x - 4} = \frac{(2-\sqrt{x})(x-5)}{-(x-1)(x-4)}
]
Burada x \to 4 olduğunda (x-4) ifadesi paydanın ve belirsizliğin bir nedenidir. x \to 4 çevresinde bir sadeleştirme ihtiyacı doğar. Ancak paydaki (2-\sqrt{x}) kısmı ayrı dikkat gerektirir.
Adım 4: (2-\sqrt{x}) İfadesine Yaklaşım
x \to 4 durumunda \sqrt{x} > 0 olduğu için (2-\sqrt{x}) tanımlı kalır ve problem çözülmeden sadeleşmez. Alternatif: Numerik yaklaşım. Soruyu görselde kontrol edip teyit amaçlı tekrar sormanızı esa.