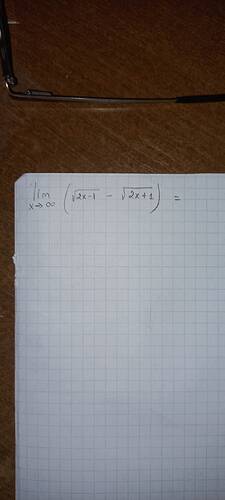Bu limit ifadesini nasıl çözeriz?
Verilen limit ifadesi:
\lim_{x \to \infty} \left( \sqrt{2x-1} - \sqrt{2x+1} \right)
Bu limiti çözerken bazı adımları izleyebilirsiniz:
-
Payda Eşleştirme ile Çarp: İfadeyi payda eşleştirmesi yaparak sadeleştirmek faydalı olabilir. Bunun için, ifadeyi eşleniği ile çarpacağız:
\lim_{x \to \infty} \frac{\left(\sqrt{2x-1} - \sqrt{2x+1}\right) \cdot \left(\sqrt{2x-1} + \sqrt{2x+1}\right)}{\sqrt{2x-1} + \sqrt{2x+1}} -
Çarpanları Yayma: Yukarıdaki çarpmalarda, çarpmayı uygulayarak payı düzenleyelim:
\lim_{x \to \infty} \frac{(2x-1) - (2x+1)}{\sqrt{2x-1} + \sqrt{2x+1}}\lim_{x \to \infty} \frac{-2}{\sqrt{2x-1} + \sqrt{2x+1}} -
Limitin Hesaplanması: Bu şekilde yazılmış ifade ile limiti hesaplayabiliriz. x sonsuza giderken, hem \sqrt{2x-1} hem de \sqrt{2x+1} yaklaşık olarak \sqrt{2x} olur:
\lim_{x \to \infty} \frac{-2}{\sqrt{2x-1} + \sqrt{2x+1}} \approx \lim_{x \to \infty} \frac{-2}{2\sqrt{2x}}= \lim_{x \to \infty} \frac{-1}{\sqrt{2x}} -
Sonuç:
\lim_{x \to \infty} \frac{-1}{\sqrt{2x}} = 0
Özet: Limitin sonucu 0’dır. İfadenin eşleniği ile çarpılarak, çapraz çarpım sonucu basit formda elde edilmiş ve limit hesaplanmıştır.