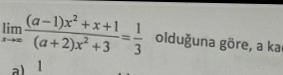
Verilen Limit Problemi Nedir?
Cevap:
Derya_Hoca’nın paylaştığı görüntüye göre, bir limit problemi verilmiştir. Bu problem şu şekildedir:
\lim_{x \to \infty} \frac{(a-1)x^2 + x + 1}{(a+2)x^2 + 3} = \frac{1}{3}
Bu limit denklemine göre, a değerini bulmamız istenmektedir.
Çözüm Aşamaları:
Adım 1: Limit Alırken İfadenin Analizi
- Verilen limit problemini analiz edelim: İfade, \lim_{x \to \infty} şeklinde bir rasyonel fonksiyon.
- Pay ve paydayı x’e göre incelersek, her iki polinomda da x² terimi baskın olacaktır.
Adım 2: Payın ve Paydanın En Büyük Terimleri
- Payda en büyük terimi ve payda en büyük terimi x²’dir.
- Bu durumda, limit alınırken en büyük terimleri inceleriz:
\lim_{x \to \infty} \frac{(a-1)x^2 + x + 1}{(a+2)x^2 + 3} = \frac{\lim_{x \to \infty}((a-1)x^2)}{\lim_{x \to \infty}((a+2)x^2)}
Adım 3: Limit Alın ve Eşitliği Sağlayın
- Bu ifadeyi sadeleştirdiğimizde:
\lim_{x \to \infty} \frac{(a-1)x^2}{(a+2)x^2} = \frac{a-1}{a+2}
- Limit verdiğimiz değere eşit olmalı:
\frac{a-1}{a+2} = \frac{1}{3}
Adım 4: Eşitliği Çözerek a Değerini Bulun
- İki tarafı çapraz çarpma veya sadeleştirerek çözebiliriz:
3(a-1) = 1(a+2)
- Dağıtım ve düzenleme işlemleri yapalım:
3a - 3 = a + 2
aüzerindeki terimleri bir araya getirerek düzenleyelim:
3a - a = 2 + 3
2a = 5
adeğerini izole edelim:
a = \frac{5}{2}
Sonuç:
Bu denkleme göre, a değeri \frac{5}{2}'dir. Matematiksel olarak ifade ettiğimizde:
[
a = \frac{5}{2}
]
Sonuç:
a’nın değeri \frac{5}{2} diye bulunur. Bu da sorunun doğru cevabıdır.