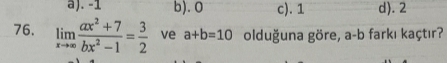
Verilen limit sorusu ne demek istiyor?
Cevap:
Bu soru, bir limit problemidir. Verilen:
\lim_{x \to \infty} \frac{ax^2 + 7}{bx^2 - 1} = \frac{3}{2}
Ayrıca, a + b = 10 koşulu verilmiş. Bu bilgileri kullanarak a - b farkını bulmamız isteniyor.
Adım 1: Limit Hesabını Anlayalım
Verilen ifadeyi incelersek, x sonsuza giderken en yüksek dereceli terimler üzerinde çalışmalıyız çünkü diğer terimler x sonsuza giderken ihmal edilebilir hale gelir. En yüksek dereceli terimler, payda ax^2 ve payda bx^2'dir.
Bu tür sorularda en yüksek dereceli terimleri ayıklayıp, pay ve payda üzerinde inceleme yaparız:
\lim_{x \to \infty} \frac{ax^2 + 7}{bx^2 - 1} \approx \lim_{x \to \infty} \frac{ax^2}{bx^2}
Bu da:
\lim_{x \to \infty} \frac{a}{b} = \frac{3}{2}
Bunu x'lerin katlarının dışarı alımı ile yaptık ve burada x \to \infty olduğundan dolayı daha düşük dereceli terimler ihmal edilmiştir.
Adım 2: Değişkenler Arasındaki İlişkileri Kullanma
Bize a + b = 10 koşulu da verilmiş, bunu ve bulduğumuz \frac{a}{b} = \frac{3}{2} eşitliğini kullanmamız gerekecek.
Öncelikle ilk durumu, yani $\frac{a}{b} = \frac{3}{2}$’yi ele alıyoruz:
- a = \frac{3}{2}b
Şimdi bu sonucu $a + b = 10$’a koyarız:
- \frac{3}{2}b + b = 10
Bu denklemden $b$’yi bulabiliriz:
- \frac{5}{2}b = 10
- b = \frac{10 \cdot 2}{5} = 4
Bu sonucu kullanarak a'yı buluyoruz:
- a = \frac{3}{2}b = \frac{3}{2} \times 4 = 6
Adım 3: a - b Farkını Bulma
Şimdi a ve $b$’nin farkını hesaplayalım:
- a - b = 6 - 4 = 2
Sonuç
a - b farkı 2’dir.
Nihai Cevap:
a - b farkı \boxed{2}'dir.