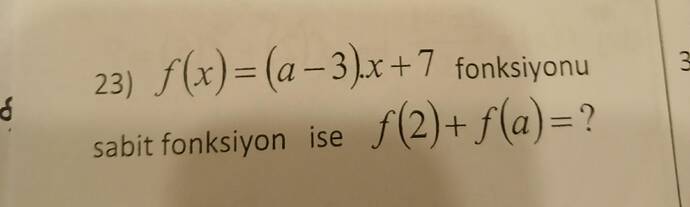Soruyu Tekrar Et:
Sevin_Cicek’in Sorusu:
Temel Kavram
Bir fonksiyonun sabit olması demek, bu fonksiyonun tanım kümesindeki tüm elemanlar için aynı değeri alması demektir. Dolayısıyla, fonksiyonun içinde bulunan değişken (bu durumda x) ne olursa olsun, sonucun değişmemesi gerekir. Bu da x'in katsayısının sıfır olması gerektiği anlamına gelir.
Temel Çözüm
Verilen fonksiyonun sabit olması için f(x) fonksiyonunun değişken x'in katsayısını sıfır yapmamız gerekir.
Adım 1: Fonksiyonun Analizi
Fonksiyon:
$$f(x) = (a - 3)x + 7$$
Adım 2: Katsayısının Sıfır Olması
Fonksiyonun sadece 7 olabilmesi, (a - 3)x teriminin kaybolması yani sıfır olmasıyla mümkündür:
$$a - 3 = 0$$
Bu denklemi çözdüğümüzde, a'yı bulabiliriz:
$$a = 3$$
Adım 3: Sabit Fonksiyonda f(x) Hesaplama
Fonksiyon artık sabit olduğu için her x için fonksiyon değeri 7 olacaktır. Bu durumda:
$$f(2) = 7$$
$$f(a) = f(3) = 7$$
f(2) + f(a) = 7 + 7 = 14
Sonuç
Bu hesaba göre, fonksiyonun sabit olması için a = 3 ve istenilen toplam f(2) + f(a) = 14 olacaktır.