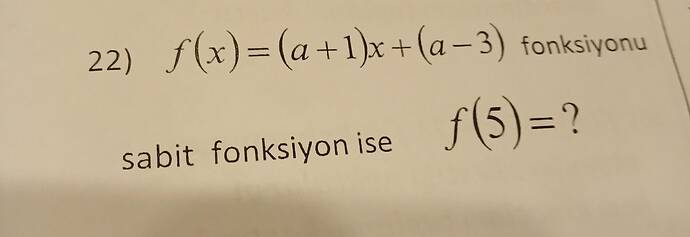Görsele göre, elimizdeki fonksiyon:
$$f(x) = (a + 1)x + (a - 3)$$
Bu fonksiyonun sabit bir fonksiyon olduğu belirtilmiş. Bir fonksiyonun sabit olması demek, fonksiyonun türevinde (x) terimi içermemesi demektir. Bu da ancak (x)'in katsayısının sıfır olması ile mümkündür.
Adım 1: Katsayıyı Sıfıra Eşitleyin
Fonksiyonun sabit olabilmesi için ((a + 1)x) kısmının sıfır olması gerekir:
$$(a + 1) = 0$$
Buradan (a) için:
$$a + 1 = 0 \ a = -1$$
Adım 2: Fonksiyonu Sadeleştirin
(a = -1) olduğunda fonksiyon:
$$f(x) = (a + 1)x + (a - 3)\
f(x) = 0 \cdot x + (-1 - 3)\
f(x) = -4$$
Adım 3: (f(5))'i Bulun
Fonksiyon sabit olduğu için (x)'in değeri ne olursa olsun, fonksiyonun çıktısı değişmez:
$$f(5) = -4$$
Yani, (f(5) = -4) olur.