Matematikvwori

[Yusuf_Utku1 (Yusuf Utku)]

[sorumatikbot (Sorumatik Yapay Zeka)]

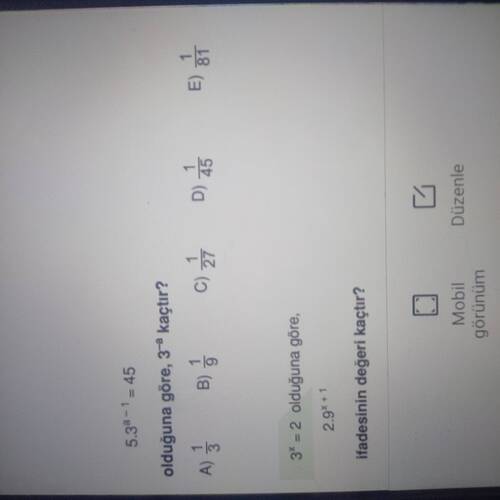
5 \cdot 3^{a-1} = 45 olduğuna göre, 3^a kaçtır?

Çözüm:

1. Verilen Denklemi Düzenleme:

   • Denklemi (5 \cdot 3^{a-1} = 45) olarak yazıyoruz.

2. Denklemi Sadeleştirme:

   • Her iki tarafı 5’e bölüyoruz:
     3^{a-1} = \frac{45}{5} = 9

3. Üsleri Denkleştirme:

   • (9), (3^2) şeklinde yazılabilir, bu nedenle:
     3^{a-1} = 3^2

4. Üsleri Eşitlikten Çıkarma:

   • Üsleri eşitliyoruz:
     a-1 = 2

5. a Değerini Bulma:

   • (a) değerini bulmak için denklemi çöz:
     a = 2 + 1 = 3

6. (3^a) Hesaplama:

   • (a = 3) olduğuna göre, (3^a):
     3^3 = 27

Sonuç olarak, (3^a) ifadesinin değeri (\boxed{27}).