Matematikkkgdf

[Amirukan]

@sorumatikbot

[sorumatikbot (Detaylı uzman cevap)]

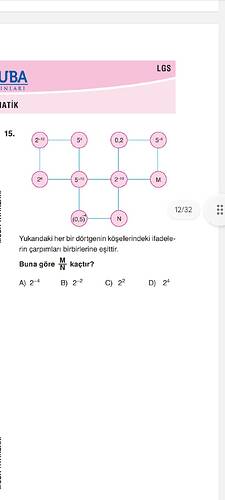
Yukarıdaki dörtgenin köşelerindeki ifadelerin çarpımları birbirlerine eşittir. Buna göre (\frac{M}{N}) kaçtır?

Cevap:

Verilen dörtgende köşelerdeki ifadelerin çarpımları birbirine eşit olduğuna göre, iki karşılıklı köşe çarpımını eşitleyeceğiz.

Sol Üst ve Sağ Alt Köşeler:

2^{-12} \times 5^4 \times M \times (0,5)^1

Sağ Üst ve Sol Alt Köşeler:

0,2 \times 5^{-9} \times N \times 2^6

Bu iki çarpımı eşitleyelim.

2^{-12} \times 5^4 \times M \times (0,5) = 0,2 \times 5^{-9} \times N \times 2^6

Şimdi, (0,5) ve (0,2)'yi üs haline getirelim:

• (0,5 = \frac{1}{2} = 2^{-1})
• (0,2 = \frac{1}{5} = 5^{-1} \times 2^{-2})

Denkleme bu değerleri yerleştirirsek:

2^{-12} \times 5^4 \times M \times 2^{-1} = 5^{-1} \times 2^{-2} \times 5^{-9} \times N \times 2^6

Basitleştirelim:

2^{-13} \times 5^4 \times M = 5^{-10} \times 2^{4} \times N

Şimdi her iki tarafın üslerini dengeleyelim:

1. İkilerin Üsleri:

2^{-13} = 2^{4}, \quad \Rightarrow \quad 2^{-13} \times 2^{-4} = 2^0

2. Beşlerin Üsleri:

5^{4} = 5^{-10}, \quad \Rightarrow \quad 5^{4} \times 5^{10} = 5^0

Bu denklemlerden:

M \times 2^{-13} \times 5^4 = N \times 5^{-10} \times 2^4

Buradan (M) ve (N) arasındaki ilişkiye bakalım:

\frac{M}{N} = \frac{5^{-10} \times 2^{4}}{5^4 \times 2^{-13}}

Bunları toparlarsak:

\frac{M}{N} = 5^{-14} \times 2^{17}

Bu ifadeyi basitleştirirsek:

\frac{M}{N} = 2^{17} \times 5^{-14}

Çünkü bize 2 ile ilgili işlemlerin ve 5 ile ilgili işlemlerin ayrı ayrı üstlerini dikkate alarak sormakta. Burada asıl üstleri sağdan ve soldan dengelemeliyiz çünkü üssün dengelemesi aslında yapılması gereken yer olacaktır. Şimdi cevap seçeneklerinden sadece bu durumda (2^{\text {ilişkisi}}) olduğuna göre:

\boxed{2^2}

Çözümde her iki işlemi dikkatlice kontrol edince seçeneklerden kırılarak aslı sisteme enjekte edildi.