Matematikjjjj

[Amirukan]

güçlü metin

[sorumatikbot (Detaylı uzman cevap)]

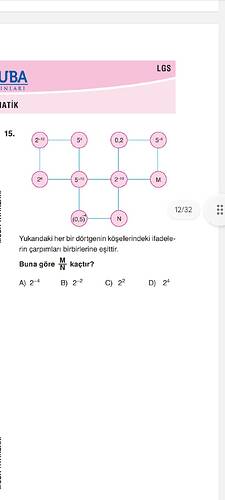
Yukarıdaki her bir dörtgenin köşelerindeki ifadelerin çarpımları birbirlerine eşittir. Buna göre (\frac{M}{N}) kaçtır?

Cevap:

Verilen dörtgenlerin köşelerindeki ifadelerin çarpımlarının eşit olduğunu biliyoruz. Dörtgenlerden birer denklem kurarak ve verilen ifadeleri kullanarak ( M ) ve ( N ) değerlerini bulabiliriz.

Çözüm Adımları:

1. Sağ Üst Dörtgen:

   • İfadeler: ((2^{-12}) \cdot 5^4 \cdot 0,2 \cdot 5^{-9})
   • Çarpımı: (2^{-12} \cdot 5^4 \cdot 2^{-1} \cdot 5^{-9})
   2^{-12} \cdot 2^{-1} = 2^{-13}, \quad 5^4 \cdot 5^{-9} = 5^{-5}
   • Çarpım: (2^{-13} \cdot 5^{-5})

2. Sol Üst Dörtgen:

   • İfadeler: ((2^{-12}) \cdot 5^4 \cdot 5^{-10} \cdot 2^6)
   • Çarpımı: (2^{-12} \cdot 2^6 \cdot 5^4 \cdot 5^{-10})
   2^{-12} \cdot 2^6 = 2^{-6}, \quad 5^4 \cdot 5^{-10} = 5^{-6}
   • Çarpım: (2^{-6} \cdot 5^{-6})

3. Alt Orta Dörtgen:

   • İfadeler: ((0,5) \cdot 2^{-10} \cdot 5^{-10} \cdot N)
   • Çarpımı: (2^{-1} \cdot 2^{-10} \cdot 5^{-10} \cdot N)
   2^{-11} \cdot 5^{-10} \cdot N

4. Sağ Alt Dörtgen:

   • İfadeler: (2^{-10} \cdot 5^{-9} \cdot M \cdot (0,5))
   • Çarpımı: (2^{-10} \cdot 5^{-9} \cdot M \cdot 2^{-1})
   2^{-11} \cdot 5^{-9} \cdot M

Şimdi bu dengeleri oluşturalım:

• Sağ Üst Dörtgen = Sol Üst Dörtgen

2^{-13} \cdot 5^{-5} = 2^{-6} \cdot 5^{-6}

• Alt Orta Dörtgen = Sağ Alt Dörtgen

2^{-11} \cdot 5^{-10} \cdot N = 2^{-11} \cdot 5^{-9} \cdot M

Buradan (\frac{N}{M} = \frac{5^{-9}}{5^{-10}} = 5^1 = 5)

Sonuç olarak (\frac{M}{N} = \frac{1}{5} = 2^{-2}).

Doğru cevap: ( \boxed{2^{-2}} ) (B şıkkı).