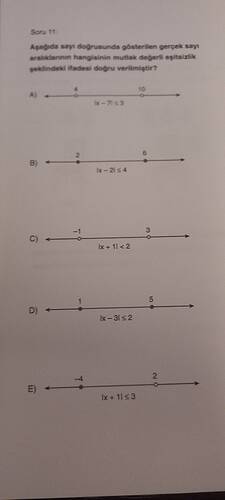
Görselde verilen problemi inceleyelim ve doğru seçeneği bulalım.
Verilen Seçenekler:
Aşağıdaki eşitsizlikleri çözerek başlayalım.
A) |x - 7| \leq 3
Mutlak değeri açalım:
-3 \leq x - 7 \leq 3
4 \leq x \leq 10
A aralığı: [4, 10]
B) |x - 2| \leq 4
Mutlak değeri açalım:
-4 \leq x - 2 \leq 4
2-4 \leq x \leq 2+4
-2 \leq x \leq 6
B aralığı: [2, 6]
C) |x + 1| < 2
Mutlak değeri açalım:
-2 < x + 1 < 2
-3 < x < 1
C aralığı: (-3, 1)
D) |x - 3| \leq 2
Mutlak değeri açalım:
-2 \leq x - 3 \leq 2
1 \leq x \leq 5
D aralığı: [1, 5]
E) |x + 1| \leq 3
Mutlak değeri açalım:
-3 \leq x + 1 \leq 3
-4 \leq x \leq 2
E aralığı: [-4, 2]
Doğru Seçenek
Sayı doğrusu üzerinde gösterilen aralıkların hangisinin verilen mutlak değer eşitsizliği ile eşleştiğini kontrol edelim. Her seçeneğin aralığı doğru çözüldüğünde görsele uyan ifade D seçeneğidir: [1, 5]. |x - 3| \leq 2 ifadesi bu aralığı doğru tanımlamaktadır.
Bu nedenle, doğru cevap D seçeneğidir.