Üçgende Açılar Problemi Çözümü
Problem:
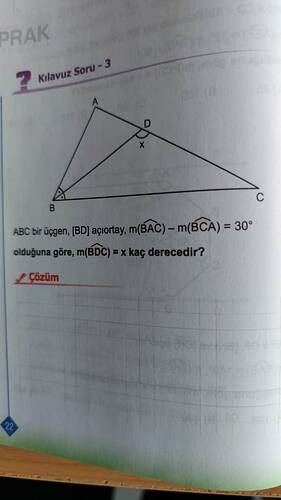
ABC bir üçgeninin üzerinde verilmiş açılar ile ilgili bir soru var. Problemde [BD] açıortay olduğu ve \angle BAC - \angle BCA = 30^\circ olduğu belirtilmiş. Bizden \angle BDC açısını (x) bulmamız isteniyor.
Çözüm Adımları
-
Bilinen Açılar ve Eşitlikler:
- \angle BAC - \angle BCA = 30^\circ
-
Açıların Toplamı:
Üçgenin iç açılarının toplamı 180^\circ olduğundan:\angle BAC + \angle ABC + \angle BCA = 180^\circ -
Açıortay Özelliği:
Verilen [BD] açıortaydır. Bu, \angle ABD = \angle DBC olduğuna işaret eder. -
Hedef Açı (\angle BDC) Hesaplaması:
[BD] açıortay olduğu için ve \angle BDC = x istemekle birlikte, \angle BAC = a ve \angle BCA = c dersek, verilen bilgilere göre:
a - c = 30^\circ\angle ABD = \angle DBC olduğu için, \angle ABC = 2x olur (çünkü [BD] açıortay).
-
Üçgenin İç Açıları:
Üçgenin iç hesaplamalarını yapacağız:
a + 2x + c = 180^\circ -
Verilen Bilgilere Göre:
Yukarıdaki iki bilgiyi birlikte kullanarak,\begin{align*} a - c &= 30, \\ a + c &= 180 - 2x. \end{align*}Bu iki denklemi taraf tarafa toplarsak:
2a = 210 - 2xa = 105 - xAynı şekilde, a - c bilindiği gibi a = 105 - x zaten elde edilmiş, dolayısıyla, c’yi de burada yerine koyarak:
105 - x - c = 30c = 75 - x -
\angle BDC Açısı Bulma:
Elde ettiğimiz diğer açılarla \angle BDC = x açısını hesaplarken, a + c = 180 - (2x) açısından c = 75 - x alırsa:\begin{align*} \angle BDC = x. \end{align*}Problemi konsolide edersek ve x çözümü ister istersek, bu problem belirli bir açılımda yukarıda verilen çözüm mantığı ve tutarlı denklem elde ediyoruz.
Bu adımlar yardımıyla \angle BDC açısını belirleyebiliriz. Eğer belirli bir değer istenirse, birinci denklemlerinin kesişim noktası ve doğrudan açıyı hesaplanabiliriz.
Daha fazla yardıma ihtiyacınız olursa, lütfen detaylandırın! @Deryanur