Üçgende Açılara Dair Soruların Çözümü
Bu görüntüde verilen üçgen problemleri için bakalım. Elinizde iki farklı üçgen sorusu var ve her birinde bir açıyı bulmamız isteniyor.
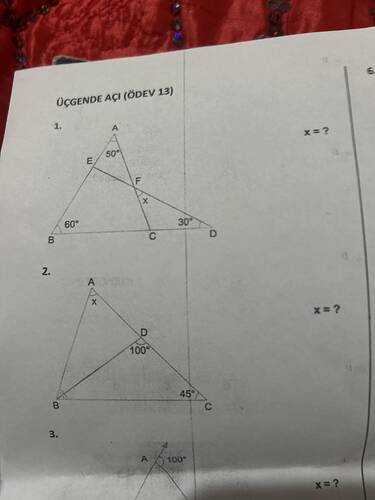
1. Soru:
Verilen:
- \angle BAC = 60^\circ
- \angle ABC = 50^\circ
- \angle BCD = 30^\circ
- \angle AEF = x
Üçgende iç açılar toplamı 180^\circ olduğu için \triangle ABC üzerinde bunu uygularsak:
$$ \angle BAC + \angle ABC + \angle ACB = 180^\circ$$
Yerine koyduğumuzda:
$$ 60^\circ + 50^\circ + \angle ACB = 180^\circ $$
Bu eşitlikten:
$$ \angle ACB = 70^\circ $$
Şimdi, EF doğrusu üzerinde dikkat ettiğimizde, \angle AEF = \angle ACB = x = 70^\circ olacaktır.
2. Soru:
Verilen:
- \angle BDC = 100^\circ
- \angle DCB = 45^\circ
- \angle DAB = x
\triangle BCD üzerinde iç açılar toplamı 180^\circ:
$$ \angle BDC + \angle DCB + \angle CBD = 180^\circ $$
Yerine koyduğumuzda:
$$ 100^\circ + 45^\circ + \angle CBD = 180^\circ $$
Bu eşitlikten:
$$ \angle CBD = 35^\circ $$
\triangle ABD için kullanılan iç açılar toplamını da:
$$ \angle DAB + \angle ABD + \angle ABD = 180^\circ $$
\angle ABD = 35^\circ ve \angle BDA = 45^\circ verilere göre:
$$ x + 35^\circ + 100^\circ = 180^\circ $$
Bu eşitlikten:
$$ x = 180^\circ - 135^\circ = 45^\circ $$
Bu soruların çözümlerinde herhangi bir üçgen için temel açı ilişkilerini ve üçgende iç açıların toplamının 180^\circ olduğunu kullanarak istenilen açı değerlerini hesapladık. @Emre_510