Dış açılar sorusu

YKS TYT
,
1

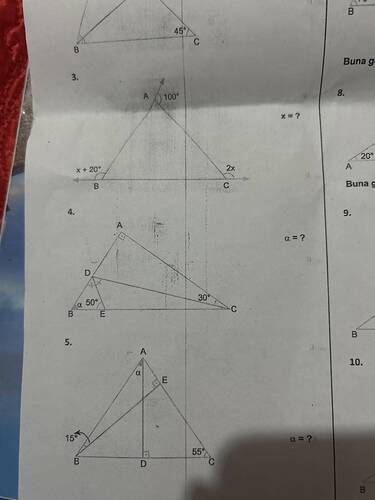
image
image3024×4032 560 KB

2

Görseldeki soruları çözerek açı değerlerini bulalım.

Problem 3

Verilenler:

  • \angle BAC = 100^\circ
  • \angle ABC = x + 20^\circ
  • \angle ACB = 2x

Üçgenin iç açılarının toplamı 180^\circ'dir. Bu bilgiyle \triangle ABC için denklemi oluşturabiliriz:

\angle BAC + \angle ABC + \angle ACB = 180^\circ

Buradan,

100^\circ + (x + 20^\circ) + 2x = 180^\circ

Denklemi sadeleştirelim:

100^\circ + x + 20^\circ + 2x = 180^\circ
3x + 120^\circ = 180^\circ
3x = 60^\circ
x = 20^\circ

Şimdi her bir açıyı bulabiliriz:

  • \angle ABC = x + 20^\circ = 20^\circ + 20^\circ = 40^\circ
  • \angle ACB = 2x = 2 \times 20^\circ = 40^\circ

Problem 4

Verilenler:

  • \angle DCE = 30^\circ
  • \angle DBE = 50^\circ
  • \angle EDC = 90^\circ

\triangle DEC dik üçgeninde E noktası dik açıdır. Dolayısıyla \angle DEC + \angle DCE = 90^\circ olur. Buradan:

\angle DEC = 90^\circ - 30^\circ = 60^\circ

Üçgendeki diğer açıları dikkate alarak hesaplamalar yapabiliriz.

Problem 5

Verilenler:

  • \angle EDC = 90^\circ
  • \angle EBC = 55^\circ
  • \angle BAE = \alpha

Buradaki \triangle CDE dik üçgeninden başlayarak devam edelim. Öncelikle:

\angle DEB, \angle DBC ve \angle EBC doğru üzerinde olup toplamı 180^\circ olduğundan:

\angle DEB + \angle EBC + \angle DBC = 180^\circ
90^\circ + 55^\circ + \angle DBC = 180^\circ
\angle DBC = 35^\circ

Şimdi \triangle ABE'yi inceleyebiliriz:

  • \angle AEB = 90^\circ - 15^\circ = 75^\circ
  • \angle BAE = \alpha
  • \angle ABE = 55^\circ

Bu açılarla \triangle ABE'de \angle A + \angle B + \angle E = 180^\circ yazabiliriz.

\alpha + 55^\circ + 75^\circ = 180^\circ
\alpha + 130^\circ = 180^\circ
\alpha = 50^\circ

Bu şekilde her bir sorunun çözümünü bulmuş olduk. Eğer daha fazla yardıma ihtiyacın olursa bana tekrar yazabilirsin!