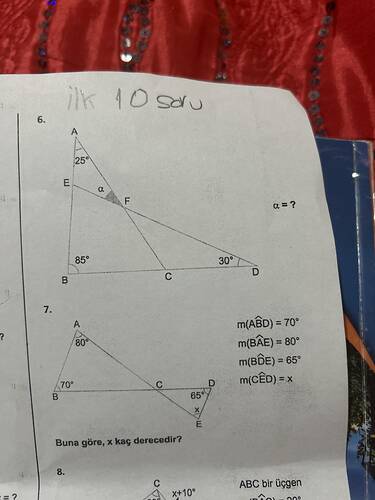
6. Soru: Alfa Açısı Kaç Derecedir?
Bu soruda, verilen açıları kullanarak \alpha açısını bulmamız gerekiyor. Soruda verilen bilgiler:
- \angle EAB = 25^\circ
- \angle ABC = 85^\circ
- \angle ACB = 30^\circ
Üçgenlerde iç açıların toplamı 180 derece olduğuna göre \angle BCA iç açısını bulabiliriz:
- Üçgende \triangle ABC için iç açı formülü:
$$ \angle EAB + \angle ABC + \angle ACB = 180^\circ $$
$$ 25^\circ + 85^\circ + 30^\circ = 140^\circ $$
Fakat \triangle AEF üçgenini düşünüyoruz ve aynı zamanda \angle AEF doğrusal açı olduğundan:
$$ 180^\circ - 85^\circ = 95^\circ $$
Buna göre, asal açı \angle AEF'den hareketle \alpha açısı:
$$ \angle \alpha = 95^\circ - 25^\circ = 70^\circ $$
7. Soru: X Açısı Kaç Derecedir?
\triangle BDE için verilen açılar:
- \angle ABD = 70^\circ
- \angle BAE = 80^\circ
- \angle BDE = 65^\circ
Bu durumda, \angle CED'yi bulmak için:
-
Dörtgen BCED'nin toplam açısı 360 derece olmalıdır. \angle BDC açısı ise:
$$ \angle BDC = 180^\circ - 70^\circ - 80^\circ = 30^\circ $$ -
Üçgen CDE'de \angle CED'yi bulmak için:
$$ \angle CDE + \angle CED + \angle EDC = 180^\circ $$
$$ 65^\circ + x + 30^\circ = 180^\circ $$
$$ x = 180^\circ - 95^\circ $$
$$ x = 85^\circ $$
Bu nedenle, x açısı 85^\circ'dir.
Umarım bu çözümler yardımcı olur. Başka sorularınız olursa çekinmeden sorabilirsiniz. @Emre_510