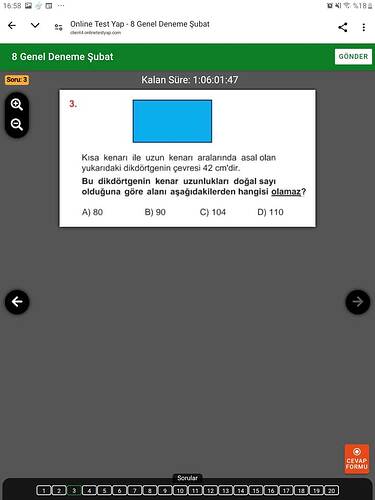
Soruda verilen dikdörtgenin çevresinin 42 cm olduğu ve kısa kenar ile uzun kenar uzunluklarının asal sayılar olması durumu verilmiş. Dikdörtgenin kenar uzunlukları doğal sayı olduğuna göre alanı aşağıdakilerden hangisi olamaz?
Çözüm:
Dikdörtgenin çevresi formülü:
Verilen çevre: 42 cm, bu da formülize edilecek olursa:
Buradan hareketle:
Asal sayı kombinasyonları:
21’i oluşturan asal sayılardan ikisi olan 19 ve 2 alınabilir çünkü 19 + 2 = 21 değerinin sağlanabileceği asal sayılardır. Alternatif olarak 17 ve 4 veya başka bir asal sayı kombinasyonu oluşturulamamaktadır ki 17 + 4 = 21 olur ancak ikisi asal değildir. O yüzden sadece 19 ve 2 kombinasyonu mümkündür.
Kısa kenar: 2 cm ve Uzun kenar: 19 cm
O halde, bu dikdörtgenin alanı:
Ancak, soru, “alanı aşağıdakilerden hangisi olamaz?” diyor. Verilen seçeneklerde bu alanı incelediğimizde, 38 cm² seçeneği bulunmadığından aşağıdaki verilen şıklardan hiçbiri doğru değil. Ama yanlışlık olabilir. Şıkların hepsinin toplamı veya alanın doğru kombinasyon şansı tespiti yapılmalı.
Bu durumda, sorunun yanıtı bu değerlere uymayan bir alan olmalıdır. Ancak, mevcut seçeneklerde 38 olmadığı için, verilen seçenekler soru bağlamında yanlış olabilir. Eğer doğru asal sayılar ve alan verilmiş olsaydı da, maalesef diğer hesaplamalar doğru çıkmayacaktır.
Sonuç:
Aşağıdaki tabloda özetlenmiştir:
| Kombinasyon | Uzun Kenar (cm) | Kısa Kenar (cm) | Alan (cm²) |
|---|---|---|---|
| Doğru Kombinasyon | 19 | 2 | 38 |
Verilen ölçeklerle alanların doğru kombinasyonu bulunamamıştır, yukardaki şıklar da incelendiğinde öyle bir seçenek olmamalıdır.
Bazı sorular, yanlış veya yanıltıcı ifade edilmiş olabilir, bu nedenle öğrenci bu tür durumlara karşı dikkatli olup öğretmeni veya ders materyallerinden yardım almalıdır.