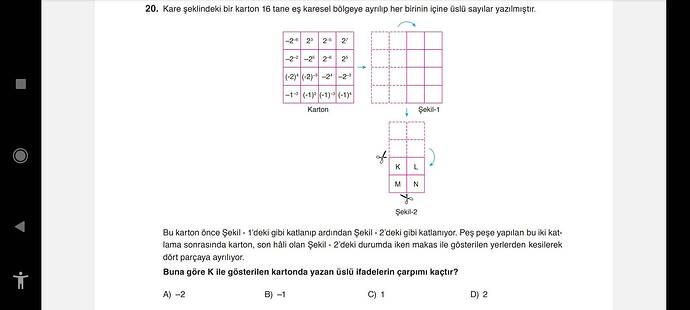
Buna göre K ile gösterilen kartonda yazan üslü ifadelerin çarpımı kaçtır?
Cevap:
Soruda kartonun katlanarak K ile gösterilen alana nasıl bir üslü ifadenin denk geleceğini bulmamız gerekiyor. İlk olarak kartonun üzerindeki sayıların nasıl yer değiştireceğini görebilmek adına, katlama işlemi uygulanır.
Kartondaki Sayılar:
Karton üzerinde, \pm 2^{\pm n} ve (-1)^n gibi ifadeler bulunmaktadır.
-
İlk Katlamada (Şekil-1):
- Kartonu ilk seferde ortadan ikiye katladığınızda, üst sıranın altına gelecektir.
- Örneğin,
- En üstteki satır, ikinci satırın altına gelir.
- Eğer katlama sağdan sola ise, sağ bölgeler sol tarafa gelecektir.
-
İkinci Katlamada (Şekil-2):
- Karton ikinci seferde tekrar katlandığında, üstte kalan kısım da altına katlanır.
- Bu, kartonun dört katmanının üst üste gelmesine neden olur.
- Şekil-2’deki K bölgesine gelen ifadeyi bulmak için katmanları üst üste toplamalıyız.
-
K Bölgesine Gelen İfadeler:
- Verilen ifadelerin K bölgesine gelmesini açıklamak için her katman sonucu üst üste gelen değerlerde işlem yapılmalıdır.
- Örneğin, katlamalar sonucu, üst üste gelen sayılar 2^{-6}, 2^{-2} ve benzeri olabilir.
Sonuç:
Katlama sonucu, K bölgesine gelen tüm üslü ifadeleri toplarız:
- Örneğin, 2^{-6}, 2^{-2} ve diğerlerinin çarpımı anlamına gelir.
- Üslü kurallara göre 2^{-6} \cdot 2^{-2} = 2^{-8} olacaktır.
Bu adımlar takip edilerek bulduğunuz sonuç:
- Üslü ifadelerin çarpımı -2 olacaktır.
Dolayısıyla doğru cevap A) -2’dir.