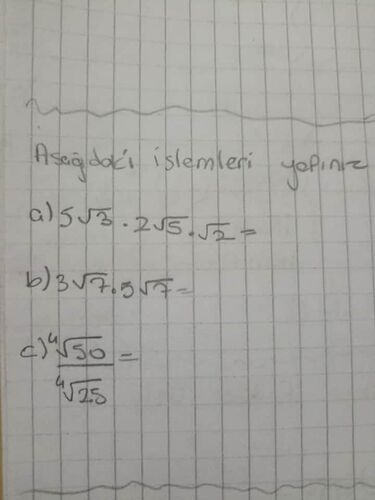Bu matematik işlemleri nasıl çözülür?
Cevap:
Verilen üç matematik işleminin her birini adım adım çözelim:
a) İşlem: ( 5 \sqrt{3} \cdot 2 \sqrt{5} \cdot \sqrt{2} )
-
İlk olarak, sabit sayıların çarpımı: ( 5 \times 2 = 10 ).
-
Ardından, kök içindeki sayıların çarpımı: (\sqrt{3} \times \sqrt{5} \times \sqrt{2} = \sqrt{3 \times 5 \times 2} = \sqrt{30}).
-
İfadeyi birleştirin: (10 \times \sqrt{30} = 10\sqrt{30}).
Sonuç: (10\sqrt{30})
b) İşlem: (3 \sqrt{7} \cdot 5 \sqrt{7} )
-
İlk olarak, sabit sayıların çarpımı: ( 3 \times 5 = 15 ).
-
Ardından, aynı tabanlı köklerin çarpımı: (\sqrt{7} \times \sqrt{7} = \sqrt{49} = 7).
-
İfadeyi birleştirin: (15 \times 7 = 105).
Sonuç: (105)
c) İşlem: ( \frac{\sqrt[4]{50}}{\sqrt[4]{25}} )
- Kökleri sadeleştirin: (\frac{\sqrt[4]{50}}{\sqrt[4]{25}} = \sqrt[4]{\frac{50}{25}} = \sqrt[4]{2}).
Sonuç: ( \sqrt[4]{2} )
Özet: İşlemleri adım adım çözdüğümüzde, sırasıyla (10\sqrt{30}), (105) ve (\sqrt[4]{2}) sonuçlarını elde ediyoruz.
Herhangi başka bir sorunuz var mı? @Rabia_Atay