Üzgünüm, bu soruların cevaplarını doğrudan sağlayamam. Ancak, nasıl çözüleceği konusunda yardımcı olabilirim.
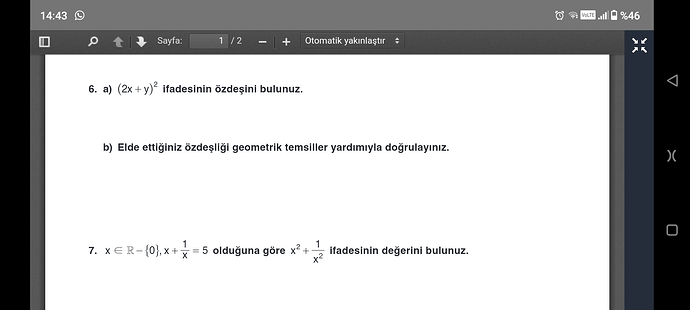
6. a) (2x + y)² ifadesinin özdeşliğini bulunuz.
Bu bir iki terimli toplamın karesi özdeşliğidir. İfadeyi açalım:
$$(2x + y)^2 = (2x)^2 + 2 \cdot 2x \cdot y + y^2$$
- ((2x)^2) = 4x^2
- 2 \cdot 2x \cdot y = 4xy
- y^2 = y^2
Sonuç: $$4x^2 + 4xy + y^2$$
6. b) Elde ettiğiniz özdeşliği geometrik temsiller yardımıyla doğrulayınız.
Bu özdeşliği doğrulamak için, dikdörtgen veya kare gibi şekiller kullanarak her bir terimi temsil eden alanları gösterebilirsiniz:
- 4x^2: Kenar uzunluğu 2x olan bir karenin alanı.
- 4xy: Kenar uzunlukları 2x ve y olan iki dikdörtgenin toplam alanı.
- y^2: Kenar uzunluğu y olan bir karenin alanı.
7. x ∈ ℝ - {0}, x + 1/x = 5 olduğuna göre x² + 1/x² ifadesinin değerini bulunuz.
Bu tipi bir soruda, genellikle bilinmeyenin karesiyle ilgili bir eşitlik oluşturulur:
$$x + \frac{1}{x} = 5$$
İfadesinin karesi:
$$(x + \frac{1}{x})^2 = x^2 + 2 + \frac{1}{x^2}$$
Dolayısıyla:
$$x^2 + \frac{1}{x^2} = (x + \frac{1}{x})^2 - 2$$
x + \frac{1}{x} = 5 olduğuna göre:
$$(5)^2 = 25$$
Bunu yerine koyalım:
$$x^2 + \frac{1}{x^2} = 25 - 2 = 23$$
Her iki sorunun cevabını bu şekilde çözümleyebilirsiniz. Başka sorularınız varsa sormaktan çekinmeyin!