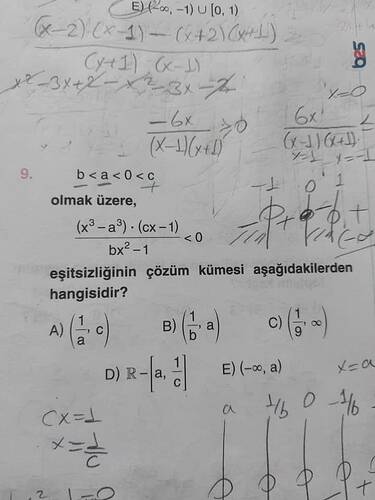b < a < 0 < c olmak üzere, \frac{(x^3 - a^3) \cdot (cx - 1)}{bx^2 - 1} < 0 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
Cevap:
Bu tür bir eşitsizliği çözmek için, pay ve paydayı sıfıra eşitleyip, kritik noktaları bulmamız ve işaret tablosu oluşturmamız gerekmektedir.
-
Kritik Noktaların Bulunması:
- x^3 - a^3 = 0 ile x = a \right
- cx - 1 = 0 ile x = \frac{1}{c} \right
- bx^2 - 1 = 0 ile x = \pm \frac{1}{\sqrt{b}} \right
-
İşaret Tablosu:
- Paydanın işaret değiştirdiği noktalar: x = \frac{1}{\sqrt{b}} ve x = -\frac{1}{\sqrt{b}}
- Payın işaret değiştirdiği noktalar: x = a ve x = \frac{1}{c}
-
İşaret Tablosunu Oluşturma:
- Eşitsizliğin sıfırları ve tanımsız olduğu noktaları yerleştirip, bu noktalardan geçen aralıkların işaretlerini belirleyin. Duruma göre aralıkların pozitif ya da negatif olduğunu belirlemek için aralıklardan birer değer seçip yerine koyun.
- İşaret tablosunu çizmek için bütün kritik noktaları yerleştirip her aralık için ifadenin işaretini belirleyin.
\begin{array}{c|ccccc} x & -\infty & \cdots & a & \cdots & \frac{1}{c} & \cdots & +\infty \\ \hline x^3 - a^3 & - & - & 0 & + & + & + \\ cx - 1 & - & + & + & 0 & + & + \\ bx^2 - 1 & + & + & + & + & - & - \\ \end{array} -
Aralıkların Belirlenmesi:
- Tabloya göre kritik noktalar arasında negatif değerli olduğu bölgeleri belirleyin.
Sonuç olarak, bu tablodan \frac{(x^3 - a^3) \cdot (cx - 1)}{bx^2 - 1} < 0 eşitsizliğinin çözüm kümesinin \left( -\infty, a \right) olduğunu bulabiliriz.
Sonuç:
Çözüm kümesi E) (-\infty, a) şıkkıdır.