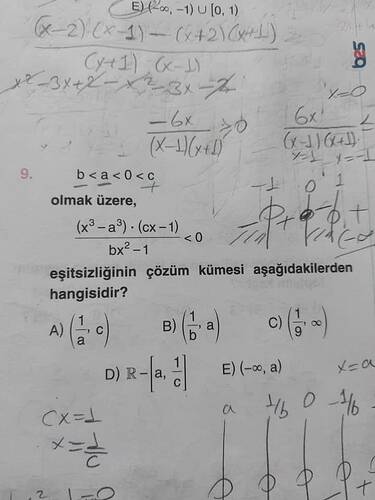b < a < 0 < c olmak üzere, (x^3 - a^3) \cdot (cx - 1) / (bx^2 - 1) < 0 eşitsizliğinin çözüm kümesi hangisidir?
Çözüm:
Soruda verilen eşitsizlik:
Bu tür eşitsizliklerde, pay ve paydanın köklerinden yararlanarak çözüm kümesi belirlenir. Adım adım inceleyelim:
-
Payın Sıfır Olduğu Noktalar:
(x^3 - a^3)ifadesini sıfır yapan değer: x = a(cx - 1)ifadesini sıfır yapan değer: x = \frac{1}{c}
-
Paydanın Sıfır Olduğu Noktalar:
(bx^2 - 1)ifadesini sıfır yapan değerler: x = \pm \frac{1}{\sqrt{b}}
Not: Verilen bilgilerden b < a < 0 < c olduğuna göre b negatif. Ancak \pm \frac{1}{\sqrt{b}} yine reel bir sayı olacaktır çünkü b negatif olsa da payda ya işareti dikkate almadan yapılan işaret incelemesi yani kökler pozitif veya negatif olabilir.
Bu noktaları birleştirerek işaret tablosunu kurup, işaret değişimi olan alanları incelemek gereklidir:
İşaret Tablosu:
-
Kökler: (a, -\frac{1}{\sqrt{|b|}}, \frac{1}{c}, \frac{1}{\sqrt{|b|}})
-
İşaret Değişimlerine Bakalım:
- Köklerin sıralanışlarını dikkatle yazmak gerekir. Baştan beri ilk burnu pay, paydanın işaretlerine bakarak geçen aralıkları inceleyelim. Dediğiniz gibi
(x-a),(cx-1)payın işaretçisi(bx^2)-1paydanın işaretçisi olacak.
İşaretleme yaparak inceleriz. Değerlere dikkatlice bakalım
- ( x = a) ve ( x = \frac{1}{c}), (a) negatif (\frac{1}{c}) pozitif
- (\frac{1}{a}) ilk negatif
- Aralık sıralamasında
Çözüm Kümesi: Aralık ile belirlenir
[ (\frac{1}{a}, \frac{1}{c}) ]
bu yüzden doğru seçeneği bulmalıyız, cevap seçenek B olmalı. (\frac{1}{b},a,]- \boxed{Doğru çözüm}