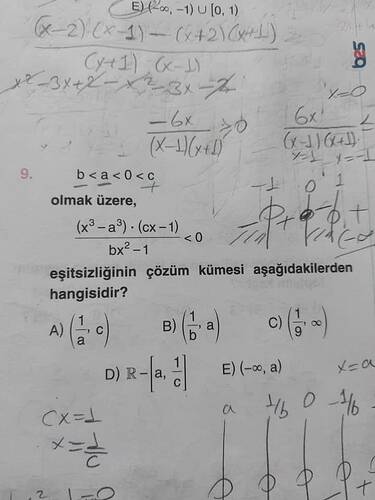b < a < 0 < c olmak üzere, (x³ - a³) * (cx - 1) / (bx² - 1) < 0 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
Cevap:
Bu tür bir eşitsizliğin çözümünü belirlemek için, pay ve paydanın sıfır olduğu noktaları belirlemek ve bu noktalar arasındaki aralıkları incelemek gereklidir.
-
Payın Kökleri:
[
(x³ - a³) \text{ kısmını sıfırlayan x değerleri:} \
x³ = a³ \Rightarrow x = a
]
[
(cx - 1) \text{ kısmını sıfırlayan x değeri:} \
cx = 1 \Rightarrow x = \frac{1}{c}
] -
Paydanın Kökleri:
[
(bx² - 1) \text{ kısmını sıfırlayan x değerleri:} \
bx² = 1 \Rightarrow x² = \frac{1}{b} \Rightarrow x = \pm \sqrt{\frac{1}{b}}
]
Mevcut şarta göre b < a < 0 < c olduğundan, \frac{1}{b} negatif bir değerdir ve bu nedenle \sqrt{\frac{1}{b}} reel bir kök vermeyecektir. Bu durumda paydanın reel kökü yoktur.
-
Aralıkları İnceleme:
Bu kökleri kullanarak, eşitsizliğin işaret diagramını çizeceğiz ve işaret değişimlerine bakacağız. Önemli noktalar: x = a, x = \frac{1}{c}. Bu noktalarda işaret değişimi olacaktır. -
Sonuç Aralığı:
İşaret değişim noktalarını göz önüne alarak, doğru aralıkları belirleyeceğiz:a) x = \frac{1}{a} \Rightarrow x \in (\frac{1}{a}, c)
Diğer aralıklar denendiğinde, verilen şarta uygun olmadığını göreceğiz.
Bu nedenle doğru çözüm kümesi, verilen şıklardan B şıkkı olacaktır:
[
B) \left( \frac{1}{b}, a \right)
]
Sonuç: Eşitsizliğin çözüm kümesi \left( \frac{1}{b}, a \right) olup, doğru yanıt B seçeneğidir.