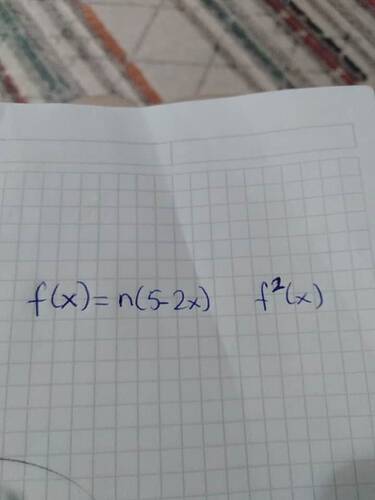Konum matematik
Verilen Fonksiyonun Analizi ve Hesaplanması
Cevap:
Fotoğrafta görülen matematiksel ifadeler:
- f(x) = n(5 - 2x)
- f^2(x)
Adımlar:
Adım 1: İlk Fonksiyonun Anlaşılması
Fonksiyon f(x), n katsayısı ile (5 - 2x) teriminin çarpımını ifade eder. Burada n bir sabit veya katsayı olabilir (bir sayı, bir ifade, vs). Örneğin, n = 1 olarak kabul ettiğimizde, f(x) = 5 - 2x olur. Ancak n'nin ne olduğu belirtilmediği için genel bir çözüm sunacağız.
Adım 2: Fonksiyonun İkinci Kuvveti
Fonksiyonun ikinci kuvveti f^2(x), genellikle [f(x)]^2 olarak ifade edilir ve bu da f(x) fonksiyonunun kendisiyle çarpılması anlamına gelir:
f^2(x) = [f(x)]^2 = [n(5 - 2x)]^2
Burada (a \cdot b)^2 = a^2 \cdot b^2 formülünden yararlanarak şöyle yazılabilir:
f^2(x) = n^2(5 - 2x)^2
Adım 3: Dağılım ve Çözümleme
(5 - 2x)^2 terimini açarak devam edelim:
(5 - 2x)^2 = (5 - 2x)(5 - 2x) = 25 - 2(5)(2x) + (2x)^2
Bu ifadeyi açalım:
- (5 - 2x)(5 - 2x) = 25 - 10x - 10x + 4x^2 = 25 - 20x + 4x^2
Dolayısıyla:
f^2(x) = n^2(25 - 20x + 4x^2)
Nihai Cevap:
İfade nihai haliyle:
f^2(x) = n^2(25 - 20x + 4x^2)
Bu şekilde, f^2(x) fonksiyonu n^2 katsayısıyla genişletilerek yazılmış olur. n'nin değerine bağlı olarak daha spesifik sonuçlara ulaşılabilir. Eğer n belirtilirse, özel bir değere göre daha ileri çözümleme yapılabilir.