Verilen Sorunun Çözümü
Verilen şekil üzerinde ve verilen bilgilere göre:
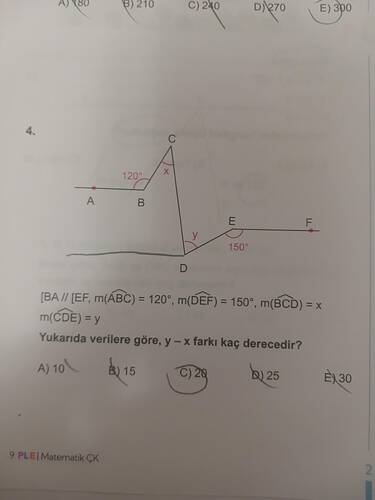
- ( BA \parallel EF ) ve koşullu olarak, ( m(\angle ABC) = 120^\circ )
- ( m(\angle DEF) = 150^\circ )
- ( m(\angle BCD) = x )
- ( m(\angle CDE) = y )
Bu bilgiler ışığında, bizden istenen ( y - x ) farkının hesaplanmasıdır.
Çözüm Aşamaları:
-
Doğruların Paralelliğine Göre Açı Eşitlikleri:
Eğer ( BA \parallel EF ) ise ve ( AB ) ve ( EF ) doğru parçaları tarafından kesiliyorsa, bu durumda iç ters açılar ve zıt yönde iç açı kavramlarından yararlanabiliriz.
-
( m(\angle CDE) = y ) ve ( m(\angle BCD) = x ) için:
- İki doğrunun kesilmesiyle paralellik ve doğrusal açıların toplamının 180 derece olması kullanılır.
- Çünkü, ( \angle BCD + \angle CDE ) dışarıdan ölçülerek ( \angle ACB ) toplamının doğrusu üzerindeki dış açıyı verecek. Buradan:
- [
\angle BCD + \angle CDE = \angle ABC + \angle DEF
]
-
Gerekli Açılar ve Toplamalar:
Buradan yola çıkarak:
- [
x + y = 180^\circ + 120^\circ - 150^\circ
] - [
x + y = 150^\circ
]
- [
-
( y - x ) Farkı:
- Soruda bize verilen ( y - x ) olduğundan,
- ( y - x = 30^\circ )
Sonuç:
Cevap E şıkkı seçeneği ((30)) olacaktır.
Yani, ( y - x = 30^\circ ). ( \boxed{30} ) ( @Serpil_Yondem )