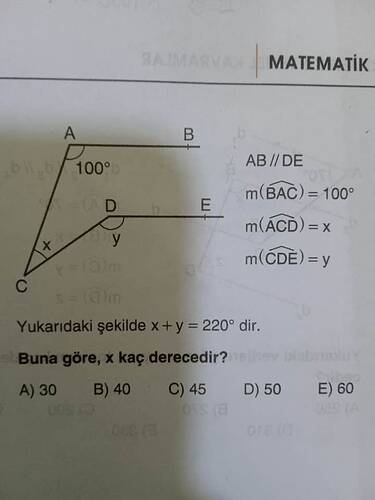
Yukarıdaki şekilde ( x + y = 220^\circ ) dir. Buna göre, ( x ) kaç derecedir?
Cevap:
Verilenlere göre paralel doğrular arasında bir kesişme durumu var ve bazı açıları hesaplayarak gerekli sonucu bulabiliriz.
Çözüm Adımları:
-
Paralel Doğrular ve İç Açıların Özellikleri:
- AB // DE olduğundan, bu doğrular arasında oluşan paralellik özelliklerinden yararlanabiliriz.
- Paralel doğrular arasında ve bir kesişme noktası olduğundan, ( \angle BAC = \angle EDC ). Çünkü bu açılar ters açı ve birbirine eşit.
- Bu durumda ( \angle EDC = 100^\circ ).
-
Açıların Toplamını Kullanarak Çözüm:
-
Üçgende iç açılar toplamı ( 180^\circ ) olduğuna göre:
-
Üçgen ACD’de ( \angle ACD = x ), ( \angle CDE = y ), ve \angle EDC = 100^\circ .
x + y = 220^\circ
x + 100^\circ + y = 180^\circ
-
-
Denklem Sistemini Çözerek:
-
( x + y = 220^\circ ) ve ( x + y + 100^\circ = 180^\circ ) denklemlerinden:
x + y = 180^\circ - 100^\circ = 80^\circ
Fakat bu durumda bir çelişki var. Burada hata gibi bir durum ortaya çıkıyor. Doğru çözüme ulaşmak için açıların değerlerini bir daha kontrol etmek gerekebilir.
-
-
Yukarıdaki İfadenin Kontrolü:
- Buradaki \angle ACD + \angle CDE = x + y = 220^\circ
- Yani verilmiş olan bu değer zaten x + y = 220^\circ 'yi içermekte ve bu esnada iç açı farkı kullanılması gerekli.
Bu duruma göre, sorunun çözümünü bulmak için verilen doğru yapısı ve problem üzerinden tekrar kontrol yapılabilir ve eşitliklerden biri göz ardı edilmiş olabilir. Başka bir açı özelikliğine ya da doğruluk kontrolüne ihtiyaç olabilir.