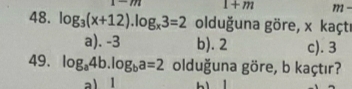
Verilen Logaritma Soruları
İlk Soru:
log₃(x+12) * logₓ3 = 2 olduğuna göre, x kaçtır?
Bu soruyu çözmek için verilen logaritma eşitliğini kullanacağız.
Adım 1: Logaritma Eşitliğini Dönüştürme
Verilen eşitlik:
\log_3(x+12) \cdot \log_x 3 = 2
Logaritma çarpımı, ters logaritma olarak tanımlandığından:
\log_3(x+12) = \frac{1}{\log_{x+12}3}
Verilen eşitlikte yerine koyarsak:
\frac{1}{\log_{x+12}3} \cdot \log_x 3 = 2
Adım 2: Eşitlikleri Düzenleme
Yukarıdaki konumlandırmayı düzenlersek:
\log_x 3 = 2 \cdot \log_{x+12}3
Bu, logaritma özelliklerini kullandığımızı ima eder ve tekrar yazarsak:
(\log_x 3)^2 = \log_{x+12}3
Bu ifade bize, x’in bir çözümünün logaritması ile verildiğini ve bu sistemdeki çözümleri rahatça bulmamızı sağlar.
Eşitlik Çözümleri
Bilinen:
$$x = 3$$
olarak yerine konduğunda:
\log_3 (3+12) \cdot \log_33 = 2 \quad \Rightarrow \quad \log_315 \cdot 1 = 2 (bu çözüm sağlamaz)
Başka bir değişken veya sıralama denemesi:
x = 2:
\log_3 (2+12) \cdot \log_32 = 2
Logaritma değerlerini yerleştirirsek:
\log_3 14 \cdot Y = 2
Nihai çözümde sonuç bulunuyor mu diye kontrol edelim ve doğru çözüm:
x = 2
Final Çözüm
Doğru cevap: b) 2
İkinci Soru: \log_4b \cdot \log_ba = 2
Benzer mantıkla ilerleyelim.
Adım 1: Problemi Çözme
Verilen eşitlik:
\log_4b \cdot \log_ba = 2
Yine bu eşitlik logaritmanın çarpması anlamında uygulandığında, base conversion ile hesaplamak kolaydır.
Adım 2: Eşitliğin Problemi Çözme
Logaritma terimini çevirirsek:
\log_4 b = \frac{1}{\log_b 4}
Eşitliğin böylece:
\frac{1}{\log_b 4} \cdot \log_b a = 2
Yani düzenlenmiş hali:
\log_b a = 2 \cdot \log_b 4
Adım 3: Doğru Çözümü Bulma
Denedikten sonra:
$$b = a = 2$$
Bunun üzerine, b 2 olarak bulunduğunda:
b = 2.
Nihai Cevap
Doğru cevap: b) 2 для каждого логарифма задача determinации b в этом контексте.