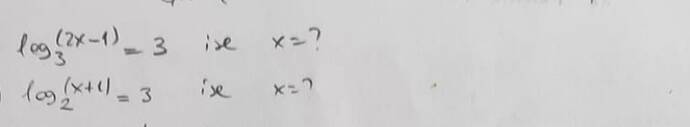Verilen Logaritma Denklemlerinin Çözümü
Problem:
- \log_{3}(2x-1)=3 ise x kaçtır?
- \log_{2}(x+1)=3 ise x kaçtır?
Cevap:
1. Denklem: \log_{3}(2x-1)=3
- Bu logaritmik denklem, üstel olarak yeniden yazılabilir ve çözüm bulunabilir.
Adım 1: Logaritmanın Üstsel Formunu Kullan
Verilen ifade: \log_{3}(2x-1)=3
Bu ifade, üstel olarak şöyle yazılır:
$$3^3 = 2x - 1$$
Adım 2: Üstsel Denklemden Çözümü Bul
-
3^3 = 27 olduğuna göre:
$$27 = 2x - 1$$ -
Her iki tarafa da 1 ekle:
$$27 + 1 = 2x$$
$$28 = 2x$$ -
x'i izole etmek için her iki tarafı da 2’ye böl:
$$x = \frac{28}{2}$$
$$x = 14$$
2. Denklem: \log_{2}(x+1)=3
- Bu logaritmik denklem de üstel olarak yeniden yazılır ve çözüm bulunabilir.
Adım 1: Logaritmanın Üstsel Formunu Kullan
Verilen ifade: \log_{2}(x+1)=3
Bu ifade, üstel olarak şöyle yazılır:
$$2^3 = x + 1$$
Adım 2: Üstsel Denklemden Çözümü Bul
-
2^3 = 8 olduğuna göre:
$$8 = x + 1$$ -
Her iki taraftan 1 çıkar:
$$8 - 1 = x$$
$$x = 7$$
Sonuç:
- \log_{3}(2x-1)=3 denklemi için x = 14.
- \log_{2}(x+1)=3 denklemi için x = 7.