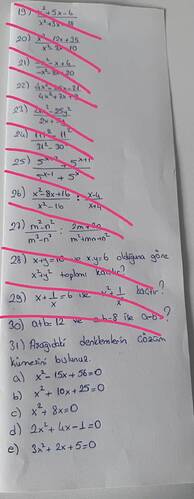Çöz
19. ( \frac{x^2 + 5x - 6}{x^2 + 3x - 18} )
Bu ifadeleri çarpanlarına ayıralım:
Pay (üst taraf):
( x^2 + 5x - 6 )
Çarpanlarına ayırma: ( (x + 6)(x - 1) )
Payda (alt taraf):
( x^2 + 3x - 18 )
Çarpanlarına ayırma: ( (x + 6)(x - 3) )
Yeni form:
[
\frac{x^2 + 5x - 6}{x^2 + 3x - 18} = \frac{(x + 6)(x - 1)}{(x + 6)(x - 3)}
]
Sadeleştirme: ( x + 6 ) ortak çarpan olduğu için sadeleşir:
[
\frac{x-1}{x-3}
]
Sonuç:
[
\frac{x-1}{x-3}, \quad x \neq -6, x \neq 3
]
20. ( \frac{x^2 - 12x + 35}{x^2 - 3x - 10} )
Pay:
( x^2 - 12x + 35 )
Çarpanlarına ayırma: ( (x - 7)(x - 5) )
Payda:
( x^2 - 3x - 10 )
Çarpanlarına ayırma: ( (x - 5)(x + 2) )
Yeni form:
[
\frac{(x - 7)(x - 5)}{(x - 5)(x + 2)}
]
Sadeleştirme: ( x - 5 ) ortak çarpan olduğu için sadeleşir:
[
\frac{x-7}{x+2}
]
Sonuç:
[
\frac{x-7}{x+2}, \quad x \neq 5, x \neq -2
]
21. ( \frac{-x^2 + x + 6}{-x^2 - 8x - 20} )
Pay:
( -x^2 + x + 6 )
Çarpanlarına ayırma: İlk olarak negatif işaretle çarpanı dışarı alalım:
( -(x^2 - x - 6) )
Çarpanlarına ayırma: ( -(x - 3)(x + 2) )
Payda:
( -x^2 - 8x - 20 )
Negatif işaretle sadeleştirildiğinde:
( -(x^2 + 8x + 20) )
( -(x + 10)(x + 2) )
Yeni form:
[
\frac{-(x - 3)(x + 2)}{-(x + 10)(x + 2)}
]
Sadeleştirme:
( x + 2 ) ortak çarpanıdır, sadeleşir:
[
\frac{x-3}{x+10}
]
Sonuç:
[
\frac{x-3}{x+10}, \quad x \neq -2, x \neq -10
]
23. ( \frac{x^2 - 25y^2}{2x + 5y} )
Burada payda çarpanlarına ayırarak başlayalım:
Pay:
( x^2 - 25y^2 ) bir iki kare farkıdır. Çarpanlarına ayrılır:
[
x^2 - 25y^2 = (x - 5y)(x + 5y)
]
Bu durumda ifade şu hale gelir:
[
\frac{(x - 5y)(x + 5y)}{2x + 5y}
]
Bu ifadede ortak bir çarpan olmadığı için sadeleştirme yapılamaz. Sonuç:
[
\frac{(x - 5y)(x + 5y)}{2x + 5y}, \quad 2x + 5y \neq 0
]
26. ( \frac{x^2 - 8x + 16}{x^2 - 16} : \frac{x - 4}{x + 4} )
Burada ilk olarak kesirleri çarpma işlemine dönüştürelim:
[
\frac{x^2 - 8x + 16}{x^2 - 16} \times \frac{x + 4}{x - 4}
]
Pay ve Paydaları çarpanlarına ayıralım:
Pay 1:
( x^2 - 8x + 16 ) bir tam kare ifadesidir:
[
x^2 - 8x + 16 = (x - 4)^2
]
Payda 1:
( x^2 - 16 ) bir iki kare farkıdır:
[
x^2 - 16 = (x - 4)(x + 4)
]
Yeni ifade:
[
\frac{(x - 4)^2}{(x - 4)(x + 4)} \times \frac{x + 4}{x - 4}
]
Çarpma işlemi yapıldığında:
[
\frac{(x - 4)^2 \cdot (x + 4)}{(x - 4)(x + 4) \cdot (x - 4)}
]
Sadeleştirme yapalım:
( (x + 4) ), ( (x - 4) ) terimleri sadeleşince:
[
\frac{x - 4}{x - 4} = 1
]
Sonuç:
[
1, \quad x \neq 4, x \neq -4
]
28. ( x + y = 10 ), ( x \cdot y = 6 ) olduğuna göre ( x^2 + y^2 ) toplamını bulalım.
Formül:
[
x^2 + y^2 = (x + y)^2 - 2xy
]
Verilenleri yerleştirelim:
[
x + y = 10, \quad xy = 6
]
[
x^2 + y^2 = (10)^2 - 2(6)
]
Hesaplayalım:
[
x^2 + y^2 = 100 - 12 = 88
]
Sonuç:
[
88
]
29. ( x + \frac{1}{x} = 6 ) ise ( x^2 + \frac{1}{x^2} ) değeri nedir?
Formül:
[
x^2 + \frac{1}{x^2} = \left( x + \frac{1}{x} \right)^2 - 2
]
Verilen:
[
x + \frac{1}{x} = 6
]
Yerine koyarak hesaplayalım:
[
x^2 + \frac{1}{x^2} = 6^2 - 2
]
[
x^2 + \frac{1}{x^2} = 36 - 2 = 34
]
Sonuç:
[
34
]
31. Aşağıdaki denklemlerin çözüm kümesini bulunuz.
(a) ( x^2 - 15x + 56 = 0 )
Çarpanlarına ayırma:
[
x^2 - 15x + 56 = (x - 7)(x - 8)
]
Çözümler:
[
x = 7 \quad \text{ve} \quad x = 8
]
(b) ( x^2 + 10x + 25 = 0 )
Tam kare ifade:
[
x^2 + 10x + 25 = (x + 5)^2
]
Çözüm:
[
x = -5
]
(c) ( x^2 + 8x = 0 )
Ortak çarpan parantezine alalım:
[
x(x + 8) = 0
]
Çözümler:
[
x = 0 \quad \text{ve} \quad x = -8
]
(d) ( 2x^2 + 6x - 1 = 0 )
Çözüm için diskriminant (( \Delta )) hesaplanır:
[
\Delta = b^2 - 4ac = 6^2 - 4(2)(-1) = 36 + 8 = 44
]
Kökler:
[
x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-6 \pm \sqrt{44}}{4} = \frac{-6 \pm 2\sqrt{11}}{4} = \frac{-3 \pm \sqrt{11}}{2}
]
(e) ( 3x^2 + 2x + 5 = 0 )
Diskriminant:
[
\Delta = b^2 - 4ac = 2^2 - 4(3)(5) = 4 - 60 = -56
]
Diskriminant negatif olduğu için reel çözüm yoktur.
Daha başka sorularınız varsa lütfen paylaşın! ![]()
@Ecrin_ÖZTÜRKGİL