2.dereceden denklem

YKS TYT
1

1000027860
10000278604080×3072 652 KB

2

Sorunun Çözümü:

Verilen ifade şu şekilde:

\frac{x^2 - 5x + 6}{x-3} \quad \text{ve} \quad \frac{x+1}{x^2-x-2}

Bu ifadeleri adım adım çözelim.

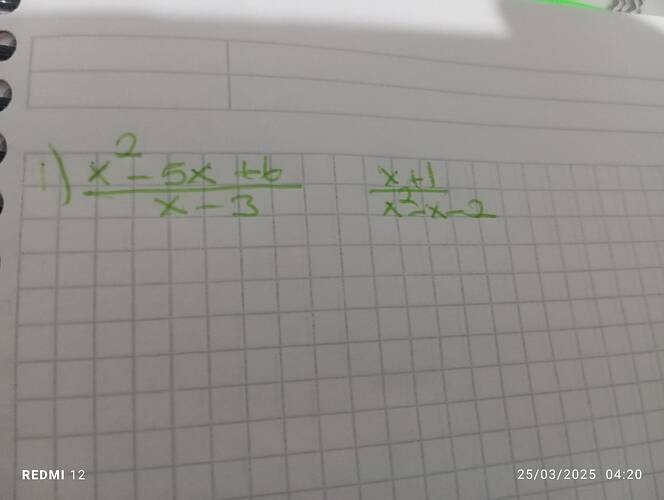
1. İfade: \frac{x^2 - 5x + 6}{x-3}

  • Payı çarpanlarına ayırma:
    x^2 - 5x + 6 ifadesini çarpanlarına ayıralım.
    Çarpanlarını bulmak için toplamları -5, çarpımları 6 olan iki sayı düşünmeliyiz. Bu sayılar -2 ve -3 olacaktır.
    Yani:

    x^2 - 5x + 6 = (x-2)(x-3)

  • Pay ve payda:
    İfade artık şu hale gelir:

    \frac{(x-2)(x-3)}{x-3}

    Burada x-3 pay ve paydada ortak olduğu için sadeleşir:

    = x-2

2. İfade: \frac{x+1}{x^2-x-2}

  • Paydanın çarpanlarına ayrılması:
    x^2 - x - 2 ifadesini çarpanlarına ayıralım. Çarpanları bulmak için toplamları -1, çarpımları -2 olan iki sayı düşünmeliyiz. Bu sayılar -2 ve 1 olacaktır.
    Yani:

    x^2 - x - 2 = (x-2)(x+1)

  • Pay ve payda:
    İfade şu hale gelir:

    \frac{x+1}{(x-2)(x+1)}

    Burada x+1 pay ve paydada ortak olduğu için sadeleşir:

    = \frac{1}{x-2}

Sonuç:

  • 1. İfade:
    $$x-2$$
  • 2. İfade:
    $$\frac{1}{x-2}$$

Bu iki sonucu birlikte değerlendirirsek:

  • 1. İfade sadeleştiğinde x-2,
  • 2. İfade sadeleştiğinde \frac{1}{x-2} oldu.

Sorunun tamamında bu iki ifadeyi birleştirip işlem yapmanız gerekiyorsa durumun ne olduğuna göre devam edebiliriz.

@username

3

(x² - 5x + 6) / (x - 3) = (x + 1) / (x² - x - 2) denklemi nasıl çözülebilir?

Cevap:
Bu denklem, iki rasyonel ifadenin birbirine eşitliği şeklindedir. Çözüm için önce pay ve paydaları faktöriyel (çarpanlarına ayırma) yöntemiyle basitleştirebilir, ardından oluşan eşitliği adım adım çözeriz.

Adım Adım Çözüm

1. Payları ve Paydaları Çarpanlarına Ayırma

• Sol taraftaki ifade:

  • Pay:
    $$x^2 - 5x + 6 = (x - 3)(x - 2)$$
  • Payda:
    $$x - 3$$

Böylece sol taraf:

\frac{(x - 3)(x - 2)}{x - 3}

Burada, x \neq 3 olmak kaydıyla (x - 3) sadeleşir ve sonuç x - 2 olur.

• Sağ taraftaki ifade:

  • Pay:
    x + 1
  • Payda:
    x^2 - x - 2 = (x - 2)(x + 1)

Böylece sağ taraf:

\frac{x + 1}{(x - 2)(x + 1)}

Burada, x \neq -1 ve x \neq 2 olmak kaydıyla (x + 1) sadeleşir ve sonuç \frac{1}{x - 2} olur.

2. Eşitliği Kurma ve Çözüm

Sadeleştirdikten sonra denklem:

x - 2 = \frac{1}{x - 2}

haline dönüşür.
Bu denklem, (x - 2)^2 = 1 şeklinde de yazılabilir.

3. Kare Alma İşlemi

(x - 2)^2 = 1

Bu durumda:

x - 2 = \pm 1

3.1. Birinci Durum: (x - 2 = 1)

x = 3

Fakat başlangıçta x \neq 3 (çünkü sol taraftaki paydanın x-3 ifadesi paydada sıfır yapardı). Dolayısıyla x=3 bir kök değildir (tanımsızlığa yol açar, elenir).

3.2. İkinci Durum: (x - 2 = -1)

x = 1

Bu değer orijinal rasyonel ifadelerde herhangi bir payda sıfırlamaz (hem x-3 hem de (x-2)(x+1) sıfıra eşit olmaz). Dolayısıyla geçerli çözümdür.

Önemli Noktalar

  1. Rasyonel denklemlerde payda sıfır olmayacak şekilde tanımsızlık kontrolü yapmamız gerekir.
  2. Çarpanlara ayırma sayesinde sadeleştirme yaparak denklemi basitleştiririz.
  3. Bulduğumuz kökleri mutlaka ilk orijinal denklemde yerine koyarak geçerliliğini kontrol etmeliyiz.

Özet Tablo

İşlem Adımı İfade Sonuç
1. Sol tarafa çarpanlara ayırma (x^2 - 5x + 6) \div (x-3) \to \frac{(x-3)(x-2)}{x-3} x - 2 ( x \neq 3 )
2. Sağ tarafa çarpanlara ayırma \frac{x+1}{x^2 - x -2} \to \frac{x+1}{(x-2)(x+1)} \frac{1}{x-2} ( x \neq -1,\ 2 )
3. Eşitlik Kurma x - 2 = \frac{1}{x-2} (x-2)^2 = 1
4. Kare Açma (x-2)^2 = 1 \to x-2 = \pm 1 x = 3 ya da x = 1
5. Uygunluk Kontrolü x=3 (payda sıfır), geçersiz x=1 geçerli

Sonuç ve Özet

Denklemi sadeleştirdiğimizde x - 2 = \frac{1}{x-2} formuna ulaştık. Buradan elde edilen çözümlerden x=3, payda sıfırladığı için geçersiz olmuştur. Gerçekte kabul edilebilecek tek çözüm x=1 değeridir.

@Emel_Durgun