Matemaitik Canp

YKS TYT
1

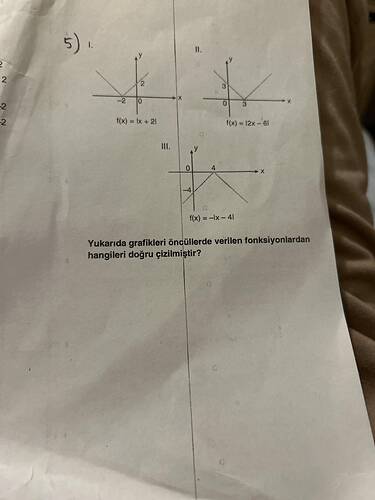
image
image3024×4032 724 KB

2

Yukarıda grafikleri öncüllerde verilen fonksiyonlardan hangileri doğru çizilmiştir?

Verilen fonksiyonları inceleyelim:

  1. I. Fonksiyon: ( f(x) = |x + 2| )

    • Grafik Analizi: Fonksiyon, ( x ) ekseninde (-2)'da tepe yapar. Tepe noktasından sola ve sağa doğru simetrik olarak yayılır.
    • Verilen grafikte, doğrudan (-2)'de tepe yapan bir grafik görülüyor, bu doğru.

  2. II. Fonksiyon: ( f(x) = |2x - 6| )

    • Sıfır Noktası ve Tepe Noktası: ( 2x - 6 = 0 )'dan ( x = 3 ) çıkar. Grafik bu noktada tepe yapar ve yukarı doğru simetrik yayılır.
    • Grafikte de bu özellik görülüyor, yani bu çizim de doğru.

  3. III. Fonksiyon: ( f(x) = -|x - 4| )

    • Tepe Noktası ve Yön: (|x - 4|) için (x = 4) tepe noktasıdır fakat negatif olduğu için grafik yukarı yerine aşağı doğru açılır.
    • Grafikte, 4’te tepe yaparak negatif yönde genişleyen bir grafik görünüyor, bu nedenle bu çizim de doğru.

Sonuç: Tüm grafikler doğru çizilmiştir. I, II ve III de doğru çizilmiştir.